|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Часть 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТРОЛОГИИ Глава 1. ПРЕДМЕТ И ЗАДАЧИ МЕТРОЛОГИИ
1.1. Метрология — наука об измерениях В практической жизни человек всюду имеет дело с измерениями. На каждом шагу встречаются измерения таких величин, как длина, объем, вес, время и др. Измерения являются одним из важнейших путей познания природы человеком. Они дают количественную характеристику окружающего мира, раскрывая человеку действующие в природе закономерности. Все отрасли техники не могли бы существовать без развернутой системы измерений, определяющих как все технологические процессы, контроль и управление ими, так и свойства и качество выпускаемой продукции. Велико значение измерений в современном обществе. Они служат не только основой научно-технических знаний, но имеют первостепенное значение для учета материальных ресурсов и планирования, для внутренней и внешней торговли, для обеспечения качества продукции, взаимозаменяемости узлов и деталей и совершенствования технологии, для обеспечения безопасности труда и других видов человеческой деятельности. Особенно возросла роль измерений в век широкого внедрения новой техники, развития электроники, автоматизации, атомной энергетики, космических полетов. Высокая точность управления полетами космических аппаратов достигнута благодаря современным совершенным средствам измерений, устанавливаемым как на самих космических аппаратах, так и в измерительно-управляющих центрах. Большое разнообразие явлений, с которыми приходится сталкиваться, определяет широкий круг величин, подлежащих измерению. Во всех случаях проведения измерений, независимо от измеряемой величины, метода и средства измерений, есть общее, что составляет основу измерений — это сравнение опытным путем данной величины с другой подобной ей, принятой за единицу. При всяком измерении мы с помощью эксперимента оцениваем физическую величину в виде некоторого числа принятых для нее единиц, т.е. находим ее значение. В настоящее время установлено следующее определение измерения: измерение есть нахождение значения физической величины опытным путем с помощью специальных технических средств. Отраслью науки, изучающей измерения, является метрология. Слово "метрология" образовано из двух греческих слов: метрон — мера и логос — учение. Дословный перевод слова "метрология" — учение о мерах. Долгое время метрология оставалась в основном описательной наукой о различных мерах и соотношениях между ними. С конца прошлого века благодаря прогрессу физических наук метрология получила существенное развитие. Большую роль в становлении современной метрологии как одной из наук физического цикла сыграл Д. И. Менделеев, руководивший отечественной метрологией в период 1892–1907 гг. Метрология в ее современном понимании — наука об измерениях, методах, средствах обеспечения их единства и способах достижения требуемой точности. Единство измерений — такое состояние измерений, при котором их результаты выражены в узаконенных единицах и погрешности измерений известны с заданной вероятностью. Единство измерений необходимо для того, чтобы можно было сопоставить результаты измерений, выполненных в разных местах, в разное время, с использованием разных методов и средств измерений. Точность измерений характеризуется близостью их результатов к истинному значению измеряемой величины. Таким образом, важнейшей задачей метрологии является усовершенствованием эталонов, разработкой новых методов точных измерений, обеспечение единства и необходимой точности измерений. 1.2. Классификация и основные характеристики измерений Измерение является важнейшим понятием в метрологии. Это организованное действие человека, выполняемое для количественного познания свойств физического объекта с помощью определения опытным путем значения какой-либо физической величины [20]. Существует несколько видов измерений. При их классификации обычно исходят из характера зависимости измеряемой величины от времени, вида уравнения измерений, условий, определяющих точность результата измерений и способов выражения этих результатов. По характеру зависимости измеряемой величины от времени измерения разделяются на • статические, при которых измеряемая величина остается постоянной во времени; • динамические, в процессе которых измеряемая величина изменяется и является непостоянной во времени. Статическими измерениями являются, например, измерения размеров тела, постоянного давления, динамическими - измерения пульсирующих давлений, вибраций. По способу получения результатов измерений их разделяют на • прямые; • косвенные; • совокупные; • совместные. Прямые — это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных. Прямые измерения можно выразить формулой Q=X, где Q — искомое значение измеряемой величины, а X — значение, непосредственно получаемое из опытных данных. При прямых измерениях экспериментальным операциям подвергают измеряемую величину, которую сравнивают с мерой непосредственно или же с помощью измерительных приборов, градуированных в требуемых единицах. Примерами прямых служат измерения длины тела линейкой, массы при помощи весов и др. Прямые измерения широко применяются в машиностроении, а также при контроле технологических процессов (измерение давления, температуры и др.). Косвенные — это измерения, при которых искомую величину определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. Значение измеряемой величины находят путем вычисления по формуле Q=F(x1, x2, …, xN), где Q — искомое значение косвенно измеряемой величины; F — функциональная зависимость, которая заранее известна, x1, x2, …, xN — значения величин, измеренных прямым способом. Примеры косвенных измерений: определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения. Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или слишком сложно измерить непосредственно или когда прямое измерение дает менее точный результат. Роль их особенно велика при измерении величин, недоступных непосредственному экспериментальному сравнению, например размеров астрономического или внутриатомного порядка. Совокупные — это производимые одновременно измерения нескольких одноименных величин, при которых искомую определяют решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин. Примером совокупных измерений является определение массы отдельных гирь набора (калибровка по известной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь). Пример. Необходимо произвести калибровку разновеса, состоящего из гирь массой 1, 2, 2*, 5, 10 и 20 кг (звездочкой отмечена гиря, имеющая то же самое номинальное значение, но другое истинное). Калибровка состоит в определении массы каждой гири по одной образцовой гире, например по гире массой 1 кг. Для этого проведем измерения, меняя каждый раз комбинацию гирь (цифры показывают массу отдельных гирь, 1обр — обозначает массу образцовой гири в 1 кг): 1=1обр+a 1+1обр=2+b 2*=2+c 1+2+2*=5+d и т.д. Буквы a, b, c, d, означают грузики, которые приходится прибавлять или отнимать от массы гири, указанной в правой части уравнения, для уравновешивания весов. Решив эту систему уравнений, можно определить значение массы каждой гири. Совместные — это производимые одновременно измерения двух или нескольких не одноименных величин для нахождения зависимостей между ними. В качестве примера можно назвать измерение электрического сопротивления при 200°C и температурных коэффициентов измерительного резистора по данным прямых измерений его сопротивления при различных температурах. По условиям, определяющим точность результата, измерения делятся на три класса: 1. Измерения максимально возможной точности, достижимой при существующем уровне техники. К ним относятся в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин, и, кроме того, измерения физических констант, прежде всего универсальных (например абсолютного значения ускорения свободного падения, гиромагнитного отношения протона и др.). К этому же классу относятся и некоторые специальные измерения, требующие высокой точности. 2. Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторого заданного значения. К ним относятся измерения, выполняемые лабораториями государственного надзора за внедрением и соблюдением стандартов и состоянием измерительной техники и заводскими измерительными лабораториями, которые гарантируют погрешность результата с определенной вероятностью, не превышающей некоторого, заранее заданного значения. 3. Технические измерения, в которых погрешность результата определяется характеристиками средств измерений. Примерами технических измерений являются измерения, выполняемые в процессе производства на машиностроительных предприятиях, на щитах распределительных устройств электрических станций и др. По способу выражения результатов измерений различают абсолютные и относительные измерения. Абсолютными называются измерения, которые основаны на прямых измерениях одной или нескольких основных величин или на использовании значений физических констант. Примером абсолютных измерений может служить определение длины в метрах, силы электрического тока в амперах, ускорения свободного падения в метрах на секунду в квадрате. Относительными называются измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную. В качестве примера относительных измерений можно привести измерение относительной влажности воздуха, определяемой как отношение количества водяных паров в 1 м³ воздуха к количеству водяных паров, которое насыщает 1 м³ воздуха при данной температуре. Основными характеристиками измерений являются: принцип измерений, метод измерений, погрешность, точность, правильность и достоверность. Принцип измерений — физическое явление или совокупность физических явлений, положенных в основу измерений. Например, измерение массы тела при помощи взвешивания с использованием силы тяжести, пропорциональной массе, измерение температуры с использованием термоэлектрического эффекта. Метод измерений — совокупность приемов использования принципов и средств измерений. Средствами измерений являются используемые технические средства, имеющие нормированные метрологические свойства. Погрешность измерений — разность между полученным при измерении X' и истинным Q значениями измеряемой величины: Δ = X'-Q Погрешность вызывается несовершенством методов и средств измерений, непостоянством условий наблюдения, а также недостаточным опытом наблюдателя или особенностями его органов чувств. Точность измерений — это характеристика измерений, отражающая близость их результатов к истинному значению измеряемой величины. Количественно точность можно выразить величиной, обратной модулю относительной погрешности: Например, если погрешность измерений равна 10-2%=10-4, то точность равна 104. Правильность измерения определяется как качество измерения, отражающее близость к нулю систематических погрешностей результатов (т.е. таких погрешностей, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины). Правильность измерений зависит, в частности, от того, насколько действительный размер единицы, в которой выполнено измерение, отличается от ее истинного размера (по определению), т.е. от того, в какой степени были правильны (верны) средства измерений, использованные для данного вида измерений. Важнейшей характеристикой качества измерений является их достоверность; она характеризует доверие к результатам измерений и делит их на две категории: достоверные и недостоверные, в зависимости от того, известны или неизвестны вероятностные характеристики их отклонений от истинных значений соответствующих величин. Результаты измерений, достоверность которых неизвестна, не представляют ценности и в ряде случаев могут служить источником дезинформации. Наличие погрешности ограничивает достоверность измерений, т.е. вносит ограничение в число достоверных значащих цифр числового значения измеряемой величины и определяет точность измерений. Глава 2. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И ИХ ЕДИНИЦЫ
2.1. Системы единиц физических величин Понятие о физической величине — одно из наиболее общих в физике и метрологии. Под физической величиной понимается свойство, общее в качественном отношении для многих физических объектов (физических систем, их состояний и происходящих в них процессов), но в количественном отношении индивидуальное для каждого объекта. Так, все тела обладают массой и температурой, но для каждого из них эти параметры различны. То же самое можно сказать и о других величинах — электрическом токе, вязкости жидкостей или потоке излучения. Для того чтобы можно было установить различия в количественном содержании свойств в каждом объекте, отображаемых физической величиной, вводится понятие размера физической величины. Исторически первой системой единиц физических величин была принятая в 1791 г. Национальным собранием Франции метрическая система мер. Она не являлась еще системой единиц в современном понимании, а включала в себя единицы длин, площадей, объемов, вместимостей и веса, в основу которых были положены две единицы: метр и килограмм. В 1832 г. немецкий математик К. Гаусс предложил методику построения системы единиц как совокупности основных и производных. Он построил систему единиц, в которой за основу были приняты три произвольные, независимые друг от друга единицы — длины, массы и времени. Все остальные единицы можно было определить с помощью этих трех. Такую систему единиц, связанных определенным образом с тремя основными, Гаусс назвал абсолютной системой. За основные единицы он принял миллиметр, миллиграмм и секунду. В дальнейшем с развитием науки и техники появился ряд систем единиц физических величин, построенных по принципу, предложенному Гауссом, базирующихся на метрической системе мер, но отличающихся друг от друга основными единицами. Рассмотрим главнейшие системы единиц физических величин [2]. Система СГС. Система единиц физических величин СГС, в которой основными единицами являются сантиметр как единица длины, грамм как единица массы и секунда как единица времени, была установлена в 1881 г. Система МКГСС. Применение килограмма как единицы веса, а в последующем как единицы силы вообще, привело в конце XIX века к формированию системы единиц физических величин с тремя основными единицами: метр — единица длины, килограмм-сила — единица силы и секунда — единица времени. Система МКСА. Основы этой системы были предложены в 1901 г. итальянским ученым Джорджи. Основными единицами системы МКСА являются метр, килограмм, секунда и ампер. 2.2. Относительные и логарифмические величины и единицы В науке и технике широко распространены относительные и логарифмические единицы измерения. Относительная величина представляет собой безразмерное отношение физической величины к одноименной физической величине, принимаемой за исходную. Логарифмическая величина представляет собой логарифм (десятичный, натуральный или при основании 2) безразмерного отношения двух одноименных физических величин. Логарифмические величины применяют для выражения уровня звукового давления, усиления, ослабления, выражения частотного интервала и т.п. Единицей логарифмической величины является бел (Б), определяемый соотношением 1Б = lg P2/P1 при P2=10P1, где P1 и P2 — одноименные энергетические величины. В случае, если берется логарифмическая величина для отношения двух одноименных "силовых" величин (напряжения, силы тока, давления, напряженности поля и т.п.), бел определяется по формуле 1Б = lg F2/F1 при F2 = √10F1. Дольной единицей от бела является децибел (дБ), равный 0,1 Б. Глава 3. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ)
3.1. Установление единой международной системы единиц Наличие ряда систем единиц физических величин, а также значительного числа внесистемных единиц, неудобства, связанные с пересчетом при переходе от одной системы единиц к другой, требовало унификации единиц измерений. Рост научно-технических и экономических связей между разными странами обусловливал необходимость такой унификации в международном масштабе. Требовалась единая система единиц физических величин, практически удобная и охватывающая различные области измерений. При этом она должна была сохранить принцип когерентности (равенство единице коэффициента пропорциональности в уравнениях связи между физическими величинами). В 1954 г. X Генеральная конференция по мерам и весам установила шесть основных единиц (метр, килограмм, секунда, ампер, кельвин и свеча) практической системы единиц. Система, основанная на утвержденных в 1954 г. шести основных единицах, была названа Международной системой единиц, сокращенно СИ (SI — начальные буквы французского наименования Systeme International). Был утвержден перечень шести основных, двух дополнительных и первый список двадцати семи производных единиц, а также приставки для образования кратных и дольных единиц. 3.2. Основные единицы СИ Основные единицы СИ с указанием сокращенных обозначений русскими и латинскими буквами приведены в табл. 1. Таблица 1
Определения основных единиц, соответствующие решениям Генеральной конференции по мерам и весам, следующие. Метр равен длине пути, проходимого светом в вакууме за 1/299792458 долю секунды. Килограмм равен массе международного прототипа килограмма. Секунда равна 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывает на каждом участке проводника длиной 1 м силу взаимодействия, равную 2·10-7 Н. Кельвин равен 1/273.16 части термодинамической температуры тройной точки воды. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0.012 кг. Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой 540·1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср. 3.3. Дополнительные единицы СИ Международная система единиц включает в себя две дополнительные единицы — для измерения плоского и телесного углов. Единица плоского угла — радиан (рад) — угол между двумя радиусами окружности, дуга между которыми по длине равна радиусу. В градусном исчислении радиан равен 57°17'48". Стерадиан (ср), принимаемый за единицу телесного угла, — телесный угол, вершина которого расположена в центре сферы и который вырезает на поверхности сферы площадь, равную площади квадрата со стороной, по длине равной радиусу сферы. Измеряют телесные углы путем определения плоских углов и проведения дополнительных расчетов по формуле Q = 2π(1–cosα/2) где Q — телесный угол; α — плоский угол при вершине конуса, образованного внутри сферы данным телесным углом. Телесному углу 1 ср соответствует плоский угол, равный 65°32', углу π ср — плоский угол 120°, углу 2π ср — плоский угол 180°. Дополнительные единицы СИ использованы для образования единиц угловой скорости, углового ускорения и некоторых других величин. Сами по себе радиан и стерадиан применяются в основном для теоретических построений и расчетов, так как большинство важных для практики значений углов (полный угол, прямой угол и т.д.) в радианах выражаются трансцендентными числами (2π, π/2 и т.д.). 3.4. Производные единицы СИ Производные единицы Международной системы единиц образуются с помощью простейших уравнений между величинами, в которых числовые коэффициенты равны единице. Так, для линейной скорости в качестве определяющего уравнения можно воспользоваться выражением для скорости равномерного прямолинейного движения v=l/t. При длине пройденного пути (в метрах) и времени t, за которое пройден этот путь (в секундах), скорость выражается в метрах в секунду (м/с). Поэтому единица скорости СИ — метр в секунду — это скорость прямолинейно и равномерно движущейся точки, при которой она за время 1 с перемещается на расстояние 1 м. Если в определяющее уравнение входит числовой коэффициент, то для образования производной единицы в правую часть уравнения следует подставлять такие числовые значения исходных величин, чтобы числовое значение определяемой производной единицы было равно единице. Например, единица кинетической энергии СИ — килограмм-метр в квадрате на секунду в квадрате — это кинетическая энергия тела массой 2 кг, движущегося со скоростью 1 м/с, или кинетическая энергия тела массой 1 кг, движущегося со скоростью √2 м/с. Эта единица имеет особое наименование — джоуль (сокращенное обозначение Дж). 3.5. Кратные и дольные единицыНаиболее прогрессивным способом образования кратных и дольных единиц является принятая в метрической системе мер десятичная кратность между большими и меньшими единицами. В табл. 2 приводятся множители и приставки для образования десятичных кратных и дольных единиц и их наименования. Таблица 2
Следует учитывать, что при образовании кратных и дольных единиц площади и объема с помощью приставок может возникнуть двойственность прочтения в зависимости от того, куда добавляется приставка. Так, сокращенное обозначение 1 км² можно трактовать и как 1 квадратный километр и как 1000 квадратных метров, что, очевидно, не одно и то же (1 квадратный километр = 1.000.000 квадратных метров). В соответствии с международными правилами кратные и дольные единицы площади и объема следует образовывать, присоединяя приставки к исходным единицам. Таким образом, степени относятся к тем единицам, которые получены в результате присоединения приставок. Поэтому 1 км² = (1 км)² = (10³ м) ² = 106 м². Глава 4. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ.
4.1. Основные понятия и определения При анализе измерений следует четко разграничивать два понятия: истинные значения физических величин и их эмпирические проявления — результаты измерений. Истинные значения физических величин — это значения, идеальным образом отражающие свойства данного объекта как в количественном, так и в качественном отношении. Они не зависят от средств нашего познания и являются абсолютной истиной. Результаты измерений, напротив, являются продуктами нашего познания. Представляя собой приближенные оценки значений величин, найденные путем измерения, они зависят не только от них, но еще и от метода измерения, от технических средств, с помощью которых проводятся измерения, и от свойств органов чувств наблюдателя, осуществляющего измерения. Разница Δ между результатами измерения X' и истинным значением Q измеряемой величины называется погрешностью измерения [17]: Δ = X' – Q (1) Но поскольку истинное значение Q измеряемой величины неизвестно, то неизвестны и погрешности измерения, поэтому для получения хотя бы приближенных сведений о них приходится в формулу (1) вместо истинного значения подставлять так называемое действительное значение. Под действительным значением физической величины мы будем понимать ее значение, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него. Причинами возникновения погрешностей являются: несовершенство методов измерений, технических средств, применяемых при измерениях, и органов чувств наблюдателя. В отдельную группу следует объединить причины, связанные с влиянием условий проведения измерений. Последние проявляются двояко. С одной стороны, все физические величины, играющие какую-либо роль при проведении измерений, в той или иной степени зависят друг от друга. Поэтому с изменением внешних условий изменяются истинные значения измеряемых величин. С другой стороны, условия проведения измерений влияют и на характеристики средств измерений и физиологические свойства органов чувств наблюдателя и через их посредство становятся источником погрешностей измерения. Описанные причины возникновения погрешностей определяются совокупностью большого числа факторов, под влиянием которых складывается суммарная погрешность измерения — см. формулу (1). Их можно объединить в две основные группы. 1. Факторы, проявляющиеся весьма нерегулярно и столь же неожиданно исчезающие или проявляющиеся с интенсивностью, которую трудно предвидеть. К ним относятся, например, перекосы элементов приборов в их направляющих, нерегулярные изменения моментов трения в опорах, малые флюктуации влияющих величин, изменения внимания операторов и др. Доля, или составляющая, суммарной погрешности измерения (1), определяемая действием факторов этой группы, называется случайной погрешностью измерения. Ее основная особенность в том, что она случайно изменяется при повторных измерениях одной и той же величины. При создании измерительной аппаратуры и организации процесса измерения в целом интенсивность проявления большинства факторов данной группы удается свести к общему уровню, так что все они влияют более или менее одинаково на формирование случайной погрешности. Однако некоторые из них, например внезапное падение напряжения в сети электропитания, могут проявиться неожиданно сильно, в результате чего погрешность примет размеры, явно выходящие за границы, обусловленные ходом эксперимента в целом. Такие погрешности в составе случайной погрешности называются грубыми. К ним тесно примыкают промахи — погрешности, зависящие от наблюдателя и связанные с неправильным обращением со средствами измерений, неверным отсчетом показаний или ошибками при записи результатов. 2. Факторы, постоянные или закономерно изменяющиеся в процессе измерительного эксперимента, например плавные изменения влияющих величин или погрешности применяемых при измерениях образцовых мер. Составляющие суммарной погрешности (1), определяемые действием факторов этой группы, называются систематическими погрешностями измерения. Их отличительная особенность в том, что они остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины. До тех пор, пока систематические погрешности больше случайных, их зачастую можно вычислить или исключить из результатов измерений надлежащей постановкой опыта. Таким образом, мы имеем два типа погрешностей измерения: • случайные (в том числе грубые погрешности и промахи), изменяющиеся случайным образом при повторных измерениях одной и той же величины; • систематические погрешности, остающиеся постоянными или закономерно изменяющиеся при повторных измерениях. В процессе измерения оба вида погрешностей проявляются одновременно, и погрешность измерения можно представить в виде суммы: Δ = δ + θ (2) где δ — случайная, а θ — систематическая погрешности. Для получения результатов, минимально отличающихся от истинных значений величин, проводят многократные наблюдения за измеряемой величиной с последующей математической обработкой опытных данных. Поэтому наибольшее значение имеет изучение погрешности как функции номера наблюдения, т. е. времени Δ(t). Тогда отдельные значения погрешностей можно будет трактовать как набор значений этой функции: Δ1(t1), Δ2(t2), … Δn(tn) В общем случае погрешность является случайной функцией времени, которая отличается от классических функций математического анализа тем, что нельзя сказать, какое значение она примет в момент времени t. Можно указать лишь вероятности появления ее значений в том или ином интервале. В серии экспериментов, состоящих из ряда многократных наблюдений, мы получаем одну реализацию этой функции. При повторении серии при тех же значениях величин, характеризующих факторы второй группы, неизбежно получаем новую реализацию, отличающуюся от первой. Реализации отличаются друг от друга из-за влияния факторов первой группы, а факторы второй группы, одинаково проявляющиеся при получении каждой реализации, придают им некоторые общие черты (рис.1). 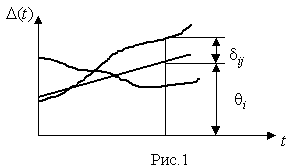 Погрешность измерений, соответствующая каждому моменту времени ti, называется сечением случайной функции Δ(t). В каждом сечении в большинстве случаев можно найти среднее значение погрешности θi, относительно которого группируются погрешности в различных реализациях. Если через полученные таким образом точки θi провести плавную кривую, то она будет характеризовать общую тенденцию изменения погрешности во времени. Нетрудно заметить, что средние значения θi определяются действием факторов второй группы и представляют собой систематическую погрешность измерения в момент времени ti, а отклонения δij от среднего в сечении, соответствующие j-й реализации, дают нам значения случайной погрешности. Последние являются уже представителями случайных величин — объектов изучения классической теории вероятностей. Предположим, что θ(ti)=0, т.е. систематические погрешности тем или иным способом исключены из результатов наблюдений, и будем рассматривать только случайные погрешности, средние значения которых равны нулю в каждом сечении. Предположим далее, что случайные погрешности в различных сечениях не зависят друг от друга, т.е. знание случайной погрешности в одном сечении как ординаты одной реализации не дает нам никакой дополнительной информации о значении, принимаемом этой реализацией в любом другом сечении. Тогда случайную погрешность можно рассматривать как случайную величину, а ее значения при каждом из многократных наблюдений одной и той же физической величины — как ее эмпирические проявления, т.е. как результаты независимых наблюдений над ней. В этих условиях случайная погрешность измерений δ определяется как разность между исправленным результатом Х измерения и истинным значением Q измеряемой величины: δ = X - Q (3) причем исправленным будем называть результат измерений, из которого исключены систематические погрешности. При проведении измерений целью является оценка истинного значения измеряемой величины, которое до опыта неизвестно. Результат измерения включает в себя помимо истинного значения еще и случайную погрешность, следовательно, сам является случайной величиной. В этих условиях фактическое значение случайной погрешности, полученное при поверке, еще не характеризует точности измерений, поэтому не ясно, какое же значение принять за окончательный результат измерения и как охарактеризовать его точность. Ответ на эти вопросы можно получить, используя при метрологической обработке результатов измерения методы математической статистики, имеющей дело именно со случайными величинами. 4.2. Описание случайных погрешностей с помощью функций распределения Рассмотрим результат наблюдений Х за постоянной физической величиной Q как случайную величину, принимающую различные значения Z, в различных наблюдениях за ней. Значения Xi будем называть результатами отдельных наблюдений. Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения [1]. Под интегральной функцией распределения результатов наблюдений понимается зависимость вероятности того, что результат наблюдения Xi в i-м опыте окажется меньшим некоторого текущего значения х, от самой величины х: Fx(x) = P(Xi ≤ x) (4) Здесь и в дальнейшем большие буквы используются для обозначения случайных величин, а маленькие — значений, принимаемых случайными величинами. Поскольку функция распределения вероятности представляет собой вероятность, то она удовлетворяет следующим свойствам: • 0 ≤ Fx(x) ≤ 1 при x ∈ (–∞, +∞), • Fx(–∞) = 0, Fx(+∞) = 1, • Fx(x) — неубывающая функция x, • P(x1 < X < x2) = FX(x2) – FX(x1). На рис.2 показаны примеры функций распределения вероятности. 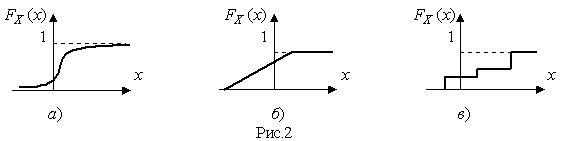 Более наглядным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей: f(x) = dFX(x)/dx (5) Физический смысл f(x) состоит в том, что произведение f(x)dx представляет вероятность попадания случайной величины Х в интервал от х до х + dx , т.е. f(x)dx = P(x ≤ X ≤ x+dx) (6) Свойства плотности распределения вероятности: иными словами, площадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс, равна единице; От дифференциальной функции распределения легко перейти к интегральной путем интегрирования: Размерность плотности распределения вероятностей, как это следует из формулы (7), обратна размерности измеряемой величины, поскольку сама вероятность — величина безразмерная. Используя понятия функций распределения, легко получить выражения для вероятностей того, что результат наблюдений Х или случайная погрешность δ примет при проведении измерения некоторое значение в интервале [x1, x2] или [δ1, δ2]. В терминах интегральной функции распределения имеем: P(x1 < X ≤ x2) = P{-∞ < X ≤ x2} – P{-∞ < X ≤ x1} = Fx(x2) – Fx(x1) P(δ1 < δ ≤ δ2) = P{-∞ < δ ≤ δ2} – P{-∞ < δ ≤ δ1} = Fδ(δ2) – Fδ(δ1) т.е. вероятность попадания результата наблюдений или случайной погрешности в заданный интервал равна разности значений функции распределения на границах этого интервала. Заменяя в полученных формулах интегральные функции распределения на соответствующие плотности распределения вероятностей согласно выражению (7), получим формулы для искомой вероятности в терминах дифференциальной функции распределения: Таким образом, вероятность попадания результата наблюдения или случайной погрешности в заданный полуоткрытый интервал равна площади, ограниченной кривой распределения, осью абсцисс и перпендикулярами к ней на границах этого интервала. Необходимо отметить, что результаты наблюдений в значительной степени сконцентрированы вокруг истинного значения измеряемой величины и по мере приближения к нему элементы вероятности их появления возрастают. Это дает основание принять за оценку истинного значения измеряемой величины координату центра тяжести фигуры, образованной осью абсцисс и кривой распределения, и называемую математическим ожиданием результатов наблюдений: В заключение можно дать более строгое определение постоянной систематической и случайной погрешностей. Систематической постоянной погрешностью называется отклонение математического ожидания результатов наблюдений от истинного значения измеряемой величины: θ = M[X] – Q (11) а случайной погрешностью — разность между результатом единичного наблюдения и математическим ожиданием результатов δ = X – M[X] (12) В этих обозначениях истинное значение измеряемой величины составляет Q = X – θ – δ (13) 4.3. Моменты случайных погрешностей Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают иногда при исследовании принципиально новых мер и измерительных приборов. Значительно чаще бывает достаточно охарактеризовать случайные погрешности с помощью ограниченного числа специальных величин, называемых моментами [3]. Начальным моментом n-го порядка результатов наблюдений называется интеграл вида представляющий собой математическое ожидание степени Xn. При n=1 т.е. первый начальный момент совпадает с математическим ожиданием результатов измерений. Центральным моментом n-го порядка результатов наблюдений называется интеграл вида Вычислим первый центральный момент: Таким образом, первый центральный момент результатов наблюдений равен нулю. Важно отметить, что начальные и центральные моменты случайных погрешностей совпадают между собой и с центральными моментами результатов наблюдений, поскольку математическое ожидание случайных погрешностей равно нулю. Особое значение наряду с математическим ожиданием результатов наблюдений имеет второй центральный момент, называемый дисперсией результатов наблюдений. При n=2 Дисперсия D[X] случайной погрешности равна дисперсии результатов наблюдений и является характеристикой их рассеивания относительно математического ожидания. Если математическое ожидание результатов наблюдений можно рассматривать в механической интерпретации как абсциссу центра тяжести фигуры, заключенной между кривой распределения и осью Ох, то дисперсия является аналогом момента инерции этой фигуры относительно вертикальной оси, проходящей через центр тяжести. Дисперсия имеет размерность квадрата измеряемой величины, поэтому она не совсем удобна в качестве характеристики рассеивания. Значительно чаще в качестве последней используется положительное значение корня квадратного из дисперсии, называемое средним квадратическим отклонением результатов наблюдений: С помощью среднеквадратического отклонения можно оценить вероятность того, что при однократном наблюдении случайная погрешность по абсолютной величине не превзойдет некоторой наперед заданной величины ε, т.е. вероятность P{|δ|}<ε. Для этого рассмотрим формулу, известную как неравенство Чебышева: Полагая ε=3σX, можно найти вероятность того, что результат однократного наблюдения отличается от истинного значения на величину, большую утроенного среднеквадратического отклонения, т.е. вероятность того, что случайная погрешность окажется больше 3σX: Вероятность того, что погрешность измерения не превысит 3σX, составит соответственно P{|δ|<ε} ≥ 1–0.11 = 0.89 Неравенство Чебышева дает только нижнюю границу для вероятности P{|δ|}<ε, меньше которой она не может быть ни при каком распределении. Обычно P{|δ|}<3σ значительно больше 0.89. Так, например, в случае нормального распределения погрешностей эта вероятность составляет 0.9973. Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют наиболее важные черты распределения: положение центра распределения и степень его разбросанности. Для более подробного описания распределения используются моменты более высоких порядков. Третий момент случайных погрешностей служит характеристикой асимметрии, или скошенности распределения. В общем случае любой нечетный момент случайной погрешности характеризует асимметрию распределения. Действительно, если распределение обладает свойством симметрии, то все функции вида δspδ(δ), где s = 1, 3, 5…, являются нечетными функциями δ (рис.3). Поэтому все нечетные моменты, являющиеся интегралами этих функций в бесконечных пределах, должны равняться нулю. Отличие этих моментов от нуля как раз и указывает на асимметрию распределения. Простейшим из нечетных моментов является третий момент μ3[δ]. Чтобы получить безразмерную характеристику, третий момент делят на третью степень среднеквадратического отклонения и получают коэффициент асимметрии, или просто асимметрию Sk распределения: 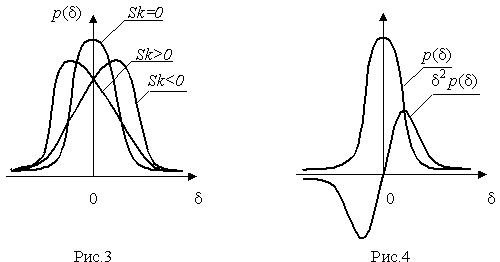 Для иллюстрации сказанного на рис. 4 приведены три кривые распределения случайных погрешностей с положительной, отрицательной и нулевой асимметрией. Четвертый момент служит для характеристики плосковершинности или островершинности распределения случайных погрешностей. Эти свойства описываются с помощью эксцесса — безразмерной характеристики, определяемой выражением Число 3 вычитают из отношения 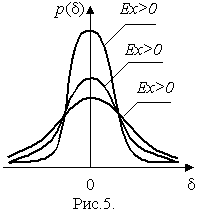 4.4. Виды распределения результатов наблюдения и случайных погрешностей Случайная погрешность измерения образуется под влиянием большого числа факторов, сопутствующих процессу измерения. В каждой конкретной ситуации работает свой механизм образования погрешности. Поэтому естественно предположить, что каждой ситуации должен соответствовать свой тип распределения погрешности. Однако во многих случаях имеются возможности еще до проведения измерений сделать некоторые предположения о форме функции распределения, так что после проведения измерений остается только определить значения некоторых параметров, входящих в выражение для предполагаемой функции распределения. Случайная погрешность характеризует неопределенность наших знаний об истинном значении измеряемой величины, полученных в результате проведенных наблюдений. Согласно К. Шеннону мерой неопределенности ситуации, описываемой случайной величиной X, является энтропия [4] являющаяся функционалом дифференциальной функции распределения pX(x). Можно предположить, что любой процесс измерения формируется таким образом, что неопределенность результата наблюдений оказывается наибольшей в некоторых пределах, определяемых допускаемыми значениями погрешности. Поэтому наиболее вероятными должны быть такие распределения pX(x), при которых энтропия обращается в максимум. Для выявления вида наиболее вероятных распределений рассмотрим несколько наиболее типичных случаев [3]. 1. В классе распределений результатов наблюдений pX(x), обладающих определенной зоной рассеивания между значениями х = b и х = а шириной b-а=2а, найдем такое, которое обращает в максимум энтропию pX(x) > 0, где Искомая плотность распределения результатов наблюдений описывается выражением Такое распределение результатов наблюдений называется равномерным. Значения дифференциальной функции распределения равномерной распределенной случайной погрешности постоянны в интервале [–а; +а], а вне этого интервала равны нулю (рис.6). 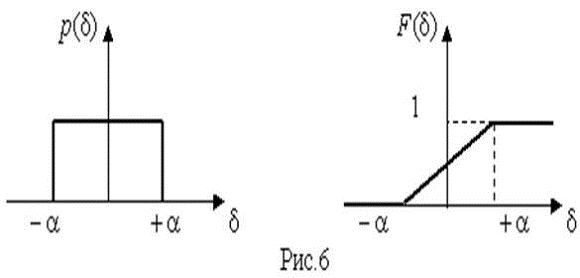 Поэтому выражение для дифференциальной функции распределения случайной погрешности можно записать в виде Определим числовые характеристики равномерного распределения. Математическое ожидание случайной погрешности находим по формуле (10): Дисперсию случайной равномерно распределенной погрешности можно найти по формуле (18): В силу симметрии распределения относительно математического ожидания коэффициент асимметрии должен равняться нулю: Для определения эксцесса найдем вначале четвертый момент случайной погрешности: поэтому В заключение найдем вероятность попадания случайной погрешности в заданный интервал [δ1, δ2], равный заштрихованной площади на рис. 7. 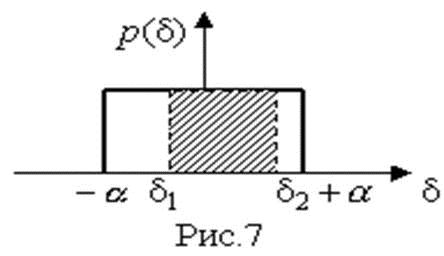 2. В классе распределений результатов наблюдений pX(x), обладающих определенной дисперсией σ²X, найдем такое, которое обращает в максимум энтропию pX(x) > 0, Решение этой задачи также находится методом множителей Лагранжа. Искомая плотность распределения результатов наблюдений описывается выражением где mX — математическое ожидание и σ²X — среднеквадратическое отклонение результатов наблюдений. Учитывая, что при полном исключении систематических погрешностей x–mX=δ и σX=σδ, для дифференциальной функции распределения случайной погрешности можно записать уравнение Распределение, описываемое уравнениями (25) и (26), называется нормальным или распределением Гаусса. На рис.8 изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратического отклонения (σ1 > σ2 > σ3). 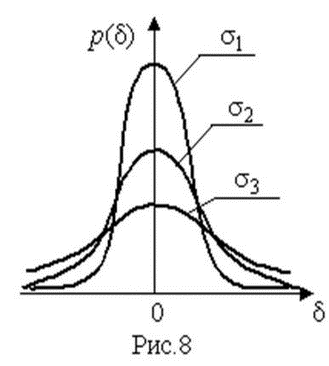 Из рисунка видно, что по мере увеличения среднеквадратического отклонения распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений. Вычислим вероятность попадания результата наблюдения в некоторый заданный интервал (x1, x2]: Заменим переменные: после чего получим следующее выражение для искомой вероятности: Интегралы, стоящие в квадратных скобках, не выражаются в элементарных функциях, поэтому их вычисляют с помощью так называемого нормированного нормального распределения с дифференциальной функцией В приложении (табл. П. 5 и П. 6) приведены значения дифференциальной функции нормированного нормального распределения, а также интегральной функции этого распределения, определяемой как С помощью функции Ф(z) вероятность P(x1 < X ≤ x2) находят как При использовании данной формулы следует иметь в виду тождество Φ(z) ≡ 1-Φ(–z) вытекающее непосредственно из определения функции Ф(z). Широкое распространение нормального распределения погрешностей в практике измерений объясняется центральной предельной теоремой теории вероятностей, являющейся одной из самых замечательных математических теорем, в разработке которой принимали участие многие крупнейшие математики — Муавр, Лаплас, Гаусс, Чебышев и Ляпунов. Центральная предельная теорема утверждает, что распределение случайных погрешностей будет близко в нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных. 3. Предположим, что результаты наблюдений распределены нормально, но их среднеквадратическое отклонение является величиной случайной, изменяющейся от опыта к опыту. Такое предположение более осторожное, чем предположение о неизменности σX в течение всего времени измерений. В этом случае, рассуждая таким же образом, как и прежде, легко найти, что энтропия обращается в максимум, если результаты наблюдений имеют распределение Лапласа с плотностью где mX — математическое ожидание, σX — среднеквадратическое отклонение результатов наблюдения. Распределением Лапласа следует пользоваться в тех случаях, когда точностные характеристики заранее неизвестны или нестабильны во времени. Дифференциальная функция распределения случайных погрешностей получается подстановкой δ=x-mX и σX=σδ в выражение (30): Асимметрия распределения равна нулю, поскольку распределение симметрично относительно нуля, а эксцесс в соответствии с формулой (22) составляет Таким образом, по сравнению с нормальным распределением (Ех = 0) равномерное распределение является более плосковершинным (Ех = -1.2), а распределение Лапласа — более островершинным (Ех = 3). 4.5. Точечные оценки истинного значения и среднеквадратического отклонения Мы подошли к решению вопроса о том, как на основании полученной в эксперименте группы результатов наблюдений оценить истинное значение, т.е. найти результат измерений, как оценить его точность, т.е. меру его приближения к истинному значению. Эта задача является частным случаем статистической задачи нахождения оценок параметров функции распределения случайной величины на основании выборки — ряда значений, принимаемых этой величиной в n независимых опытах. Оцениваемыми параметрами являются математическое ожидание и среднеквадратическое отклонение, поскольку только они входят в выражение для дифференциальных функций всех трех рассмотренных выше распределений. В уравнениях (25) и (30) для нормального распределения и распределения Лапласа эти параметры входят явно, а в уравнения (23) и (24) для равномерного распределения — не явно, поскольку α = σδ√3, b = mX+α = mX+σX√3, a = mX-α = mX-σX√3 Оценку â параметра а назовем точечной, если она выражается одним числом. Любая точечная оценка, вычисленная на основании опытных данных, является их функцией и поэтому сама должна представлять собой случайную величину с распределением, зависящим от распределения исходной случайной величины, в том числе от самого оцениваемого параметра и от числа опытов n. К точечным оценкам предъявляется ряд требований, определяющих их пригодность для описания самих параметров. 1. Оценка называется состоятельной, если при увеличении числа наблюдений она приближается (сходится по вероятности) к значению оцениваемого параметра. 2. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру. 3. Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра. На практике не всегда удается удовлетворить одновременно все эти требования, однако выбору оценки должен предшествовать ее критический анализ со всех перечисленных выше точек зрения. Существует несколько методов определения оценок. Наиболее распространен метод максимального правдоподобия, теоретически обоснованный математиком Р. Фишером. Идея метода заключается в следующем. Вся получаемая в результате многократных наблюдений информация об истинном значении измеряемой величины и рассеивании результатов сосредоточена в ряде наблюдений X1, X2, …, Xn, где n — число наблюдений. Их можно рассматривать как n независимых случайных величин с одной и той же дифференциальной функцией распределения pX(x, Q, σx). Вероятность Pi получения в эксперименте некоторого результата Xi, лежащего в интервале xi±Δx, где Δx — некоторая малая величина, равна соответствующему элементу вероятности Pi=pX(x, Q, σx)Δx. Независимость результатов наблюдений позволяет найти априорную вероятность появления одновременно всех экспериментальных данных, т.е. всего ряда наблюдений X1, X2, …, Xn как произведение этих вероятностей: Если рассматривать Q и σx как неизвестные параметры распределения, то, подставляя различные значения Q и σx в эту формулу, мы будем получать различные значения вероятности P(X1, X2, …, Xn) при каждом фиксированном ряде наблюдений X1, X2, …, Xn. При некоторых значениях Таким образом, метод максимального правдоподобия сводится к отысканию таких оценок достигает наибольшего значения. Постоянный сомножитель Δxn не оказывает влияния на решение и поэтому может быть отброшен. Полученные оценки Для упрощения вычислений иногда бывает удобнее пользоваться логарифмической функцией правдоподобия Если наибольшее значение функции правдоподобия совпадает с максимальным значением, то оценки получаются из системы уравнений В противном случае необходимо более подробное исследование функции правдоподобия. Далее определим оценки максимального правдоподобия для трех распределений случайных погрешностей, представленных в предыдущей главе. 1. Результаты наблюдений распределены нормально. В этом случае а логарифмическая функция правдоподобия в соответствии с (32) Система уравнений (33) приводится к виду Из первого уравнения получаем выражение для оценки истинного значения Таким образом, при нормальном распределении случайных погрешностей оценкой максимального правдоподобия для истинного значения является среднее арифметическое из результатов отдельных наблюдений, а оценкой дисперсии — среднее из квадратов отклонений результатов наблюдений от среднего арифметического. 2. Результаты наблюдений распределены по закону Лапласа Логарифмическая функция правдоподобия не является дифференцируемой по Q, поэтому приходится прибегать к численным методам, функция правдоподобия достигает наибольшего значения, когда выражение 3. В условиях равномерного распределения погрешностей причем a = Q–σX√3 и b = Q+σX√3. Решение задачи нахождения оценки максимального правдоподобия для равномерного распределения погрешностей проводим численными методами, в результате чего получаем: Основное достоинство оценок максимального правдоподобия в том, что они являются асимптотически (при n→∞) несмещенными; асимптотически эффективными и асимптотически нормально распределенными. Если â — оценка максимального правдоподобия для параметра а, то при достаточно большом числе n наблюдений (практически уже при n>20-25) эту оценку можно считать нормально распределенной с математическим ожиданием M[â]=a и дисперсией D[â]=(M[–∂2L/∂a2])-1 при любом распределении результатов наблюдений. Для наиболее часто встречающегося на практике нормального распределения случайных погрешностей оценки максимального правдоподобия имеются особые обозначения. Оценкой истинного значения является среднее арифметическое Вторая производная от логарифмической функции преобразования равна ∂²L/∂Q² = –n/σ²X, поэтому дисперсия среднего арифметического в n раз меньше дисперсии σ²X результатов наблюдений, т. е. Оценка дисперсии результатов наблюдений при малом n является немного смещенной, поэтому точечную оценку дисперсии принято определять как а оценку среднеквадратического отклонения результатов наблюдений как Дисперсия оценки sX среднеквадратического отклонения составляет Последнее соотношение показывает, что относительная погрешность определения среднеквадратического отклонения (в %) по результатам обработки ряда наблюдений достаточно велика: и даже при n = 50 достигает 10%. Для надежного суждения о точности эту погрешность следует увеличить еще минимум в два раза. С помощью полученных оценок итог измерений можно записать в виде что уже позволяет сделать некоторые выводы относительно точности проведенных измерений. Наряду с методом максимального правдоподобия при определении точечных оценок широко используется метод наименьших квадратов. В соответствии с этим методом среди некоторого класса оценок выбирают ту, которая обладает наименьшей дисперсией, т. е. наиболее эффективную оценку. Легко заметить, что среди всех линейных оценок истинного значения вида 4.6. Оценка с помощью интервалов Смысл оценки параметров с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенными вероятностями (доверительными) находятся истинные значения оцениваемых параметров. Вначале остановимся на определении доверительного интервала для среднего арифметического значения измеряемой величины. Предположим, что распределение результатов наблюдений нормально и известна дисперсия σ²X. Найдем вероятность попадания результата наблюдений в интервал Но и, если систематические погрешности исключены (mX = Q), Это означает, что истинное значение Q измеряемой величины с доверительной вероятностью P=2Φ(tp)–1 находится между границами доверительного интервала Половина длины доверительного интервала определяют соответствующее значение Φ(tp) интегральной функции нормированного нормального распределения. Затем по данным табл. П.3 приложения находят значение коэффициента tp и вычисляют доверительное отклонение где tp определяется по заданной доверительной вероятности Р. Полученный доверительный интервал, построенный с помощью среднего арифметического результатов n независимых повторных наблюдений, в √n раз короче интервала, вычисленного по результату одного наблюдения, хотя доверительная вероятность для них одинакова. Это говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений. Половина длины нового доверительного интервала называется доверительной границей погрешности результата измерений, а итог измерений записывается в виде Теперь рассмотрим случай, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна. В этих условиях пользуются отношением называемым дробью Стьюдента. Входящие в нее величины Плотность распределения этой дроби, впервые предсказанного Госсетом, писавшим под псевдонимом Стьюдент, выражается следующим уравнением: где S(t, k) — плотность распределения Стьюдента. Величина k называется числом степеней свободы и равна n – 1. Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале (–tp, +tp), согласно выражению (8), вычисляется по формуле или, поскольку S(t, k) является четной функцией аргумента t, Подставив вместо дроби Стьюдента t ее выражение через Величины tp, вычисленные по формулам (40) и (41), были табулированы Фишером для различных значений доверительной вероятности Р в пределах 0.10–0.99 при k = n–1 = 1,2,…,30. В табл. П.5 приведены значения tp для наиболее часто употребляемых доверительных вероятностей Р. Таким образом, с помощью распределения Стьюдента по формуле (41) может быть найдена вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает Пример. По результатам пяти наблюдений была найдена длина стержня. Итог измерений составляет L=15.785 мм, Из условия задачи следует, что имеются все основания для применения распределения Стьюдента. Вычисляем значение дроби Стьюдента и число степеней свободы k = n–1 = 5–1 = 4. По данным табл. П.4 приложения находим значение доверительной вероятности для tp = 2 и k = 4: Для tp = 3 вероятность составляет т.е несколько меньше 0.9973, как при нормальном распределении. Итог измерений удобно записать в виде L = (15.785±0.010) мм, P = 0.8838. Для tp = 1 доверительная вероятность составляет приблизительно 0.62, поэтому итог измерений можно представить также в виде L = (15.785±0.005) мм, P = 0.62, L = (15.785±0.015) мм, P = 0.96. Пример. В условиях предыдущей задачи найти доверительную границу погрешности результата измерений для доверительной вероятности P=0.99. По данным табл. П.5 при k=4 находим tp=4.604 и, следовательно, доверительная граница: Итог измерений: L = (15.785±0.023) мм, P = 0.99. При n→∞, а практически уже при n = 20–30 распределение Стьюдента переходит в нормальное распределение и где Φ(tp) — интегральная функции нормированного нормального распределения. В тех случаях, когда распределение случайных погрешностей не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной. Кроме того, на основании центральной предельной теоремы теории вероятностей можно утверждать, что при достаточно большом числе наблюдений распределение среднего арифметического как суммы случайных величин Xi/n будет сколь угодно близким к нормальному. Тогда, заменяя дисперсию σ²X ее точечной оценкой [см. п. 4.4. Нормальное распределение], можно для оценки доверительной границы погрешности результата воспользоваться равенством (35). Число наблюдений n, при котором это становится возможным, зависит, конечно, от распределения случайных погрешностей. Соотношения (38) показывают, что итог измерения не есть одно определенное число. В результате измерений мы получаем лишь полосу значений измеряемой величины. Смысл итога измерений, например, L=20.00±0.05 заключается не в том, что L = 20.00, как для простоты считают, а в том, что истинное значение лежит где-то в границах от 19.95 до 20.05. К тому же нахождение внутри границ имеет некоторую вероятность, меньшую, чем единица, и, следовательно, нахождение вне границ не исключено, хотя и может быть очень маловероятным. Теперь найдем доверительные интервалы для дисперсии и среднеквадратического отклонения результатов наблюдений. Если распределение результатов наблюдений нормально, то отношение имеет так называемое χ²-распределение Пирсона с k=n–1 степенями свободы. Его дифференциальная функция распределения описывается формулой Кривые плотности χ²-распределения при различных значениях k, вычисленные по формуле (44), представлены на рис. 9. 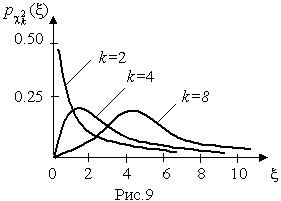 Значения χ²kp, соответствующие различным вероятностям Р того, что отношение (43) в данном опыте будет меньше χ²kp, представлены в табл. П.6 приложения для различных вероятностей Р и чисел k степеней свободы. Пользуясь этой таблицей, можно найти доверительный интервал для оценки дисперсии результатов наблюдений при заданной доверительной вероятности. Этот интервал строится таким образом, чтобы вероятность выхода дисперсии за его границы не превышала некоторой малой величины q, причем вероятности выхода за обе границы интервала были бы равны между собой и составляли соответственно q/2 (рис.10). 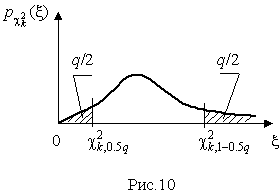 Границы χ²k,0.5q и χ²k,1–0.5q такого доверительного интервала находят из равенства F(χ²k,0.5q) = 0.5q, F(χ²k,1-0.5q) = 1-0.5q (45) Теперь, зная границы доверительного интервала для отношения χ²kp, запишем доверительный интервал для дисперсии: Полученное равенство означает, что с вероятностью α=1-q истинное значение σX среднеквадратического отклонения результатов наблюдений лежит в интервале ( Пример. Даны результаты двадцати измерений длины li мм детали (табл.3). Таблица 3
В качестве оценки математического ожидания длины детали принимаем ее среднее арифметическое Точечная оценка среднеквадратического отклонения результатов наблюдений составляет: Приняв уровень доверительной вероятности α=1-q=0.90, находим для числа степеней свободы k = n–1 = 20–1 = 19 в табл. П.6 приложения: χ²k,0.5q = χ²19,0.05 = 10.117, χ19,0.05 = 3.18, χ²k,1-0.5q = χ²19,0.95 = 30.144, χ19,0.95 = 5.49. Границы доверительного интервала для среднеквадратического отклонения результатов наблюдений находим по формуле (47): Полученные результаты говорят о том, что истинное значение среднеквадратического отклонения результатов наблюдений с вероятностью 0.90 лежит в интервале 0.0020–0.0034 мм. В табл. П.6 приведены значения χ²k только при числах степеней свободы от 1 до 30. При k>30 можно пользоваться приближенной формулой где tp определяется из условия Φ(tp)=P по табл. П.3, в которой помещены значения интегральной функции нормированного нормального распределения. Тогда границы доверительного интервала для среднеквадратического отклонения результатов наблюдений при доверительной вероятности α=1-q вычисляются по формулам (47) при значениях χk, равных Так, если в условиях предыдущей задачи среднеквадратическое отклонение определено на основании n=42 измерений, то для α=1-q=0.90 из табл. П.3 находим: t0.5q = t0.05 = –1,6449, t1-0.5q = t0.95 = +1,6449. Величины χk при k=n–1=41 составляют: Границы доверительного интервала: 4.7. Проверка нормальности распределения результатов наблюдений В предыдущих разделах было показано, что результаты наблюдений можно оценить наиболее полно, если их распределение является нормальным. Поэтому исключительно важную роль при обработке результатов наблюдений играет проверка нормальности распределения. Эта задача представляет собой частный случай более общей проблемы, заключающейся в подборе теоретической функции распределения, в некотором смысле наилучшим образом согласующейся с опытными данными. При большом числе результатов наблюдений (n>40) данная задача решается в следующем порядке. Весь диапазон полученных результатов наблюдений Xmax…Xmin разделяют на r интервалов шириной ΔXi (i=1,2,…r) и подсчитывают частоты mi, равные числу результатов, лежащих в каждом i-м интервале, т. е. меньших или равных его правой и больших левой границы. Отношения где n — общее число наблюдений, называются частостями и представляют собой статистические оценки вероятностей попадания результата наблюдений в i-й интервал. Распределение частот по интервалам образует статистическое распределение результатов наблюдений. Если теперь разделить частость на длину интервала, то получим величины являющиеся оценками средней плотности распределения в интервале ΔXi. Отложим вдоль оси результатов наблюдений (рис. 11) интервалы ΔXi в порядке возрастания индекса i и на каждом интервале построим прямоугольник с высотой, равной pi*. Полученный график называется гистограммой статистического распределения. 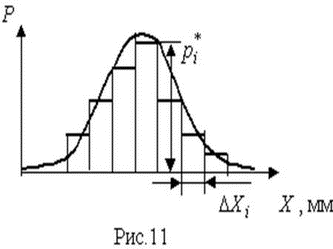 Площадь суммы всех прямоугольников равна единице: При увеличении числа наблюдений число интервалов можно увеличить. Сами интервалы уменьшаются, и гистограмма все больше приближается к плавной кривой, ограничивающей единичную площадь, — к графику плотности распределения результатов наблюдений. При построении гистограмм рекомендуется пользоваться следующими правилами: 1. Число интервалов выбирается в зависимости от числа наблюдений согласно рекомендациям табл.6. Таблица 6
2. Длины интервалов удобнее выбирать одинаковыми. Однако если распределение крайне неравномерно, то в области максимальной концентрации результатов наблюдений следует выбирать более узкие интервалы. 3. Масштабы по осям гистограммы должны быть такими, чтобы отношение ее высоты к основанию составляло примерно 5÷8. Пример. Было выполнено 100 измерений среднего диаметра резьбового калибра. Результаты наблюдений лежат в диапазоне 8.911–8.927 мм, т. е. зона распределения результатов составляет 0.016 мм. Весь диапазон удобно разделить на восемь равных интервалов через 0.002 мм. В табл. 7 приведены частоты mi, частости Pi* и плотности p* статистического распределения. Таблица 7
После построения гистограммы надо подобрать теоретическую плавную кривую распределения, которая, выражая все существенные черты статистического распределения, сглаживала бы все случайности, связанные с недостаточным объемом экспериментальных данных. Принципиальный вид теоретической кривой выбирают заранее, проанализировав метод измерения, или хотя бы по внешнему виду гистограммы. Тогда определение аналитического вида кривой распределения сводится к выбору таких значений его параметров, при которых достигается наибольшее соответствие между теоретическим и статистическим распределением. Одним из методов решения этой задачи является метод моментов. При его использовании параметрам теоретического распределения придают такие значения, при которых несколько важнейших моментов совпадают с их статистическими оценками. Так, если статистическое распределение, определяемое гистограммой, приведенной на рис. 11, мы хотим описать кривой нормального распределения, то естественно потребовать, чтобы математическое ожидание и дисперсия последнего совпадали со средним арифметическим и оценкой дисперсий, вычисленным по опытным данным. В предыдущем примере Далее законно возникает вопрос, объясняются ли расхождения между гистограммой и подобранным теоретическим распределением только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они вызваны тем, что результаты наблюдений в действительности распределены иначе? Для ответа на этот вопрос используют методы проверки статистических гипотез. Идея их применения заключается в следующем. На основании гистограммы, полученной при обработке опытных данных, строится гипотеза, состоящая в том, что результаты наблюдений подчиняются распределению FX(x) с плотностью PX(x). Для того чтобы принять или опровергнуть эту гипотезу, выбирается некоторая величина U, представляющая собой меру расхождения теоретического и статистического распределений. В качестве меры расхождения можно принять сумму квадратов разностей частостей и теоретических вероятностей попадания результатов наблюдений в каждый интервал, взятых с некоторыми коэффициентами: где tp — коэффициенты, называемые весами разрядов; Pi — теоретические вероятности, определяемые как Здесь pX(x) — предполагаемая плотность распределения. Мера расхождения U является случайной величиной и, независимо от исходного распределения подчиняется χ²-распределению с k степенями свободы — см. формулу (44). Если значения всех частот mi>5, число измерений стремится к бесконечности, а веса ci выбираются равными n/Pi. Число степеней свободы распределения k = r–s, где r — число разрядов гистограммы статистического распределения, а s — число независимых связей, наложенных на частости Pi*. Если проверяется гипотеза о нормальности распределения, то к числу этих связей относится равенство среднего арифметического математическому ожиданию, а точечной оценки дисперсии - дисперсии предполагаемого нормального распределения. Кроме того, всегда требуется, чтобы сумма частостей по всем интервалам была равна единице. Поэтому в данном случае s = 3. По табл. П.6 можно при заданной доверительной вероятности α=1-q найти тот доверительный интервал (χ²k,0.5q, χ²k,1-0.5q) значений χ²k, в который мера расхождения может попасть по чисто случайным причинам. Если вычисленная по опытным данным мера расхождения окажется в указанном интервале, то гипотеза принимается. Это, конечно, не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, т.е. не противоречит опытным данным. Если же она выходит за границы доверительного интервала, то гипотеза отвергается как противоречащая опытным данным. Поскольку проверка гипотезы основывается на опытных данных, то при принятии решения всегда возможны ошибки. Отвергая в действительности верную гипотезу, мы совершаем ошибку первого рода. Вероятность ошибки первого рода называется уровнем значимости и составляет q=1-a. Принимая в действительности неверную гипотезу, мы совершаем ошибку второго рода. Вычислить ее вероятность, вообще говоря, невозможно, поскольку для этого нужно рассмотреть все прочие возможные гипотезы, являющиеся альтернативой обсуждаемой гипотезы. Можно лишь утверждать, что при уменьшении ошибки первого рода ошибка второго рода увеличивается, поэтому не имеет смысла брать слишком высокие значения доверительных вероятностей. Описанная процедура проверки гипотезы о том, что данное статистическое распределение является распределением с плотностью pX(x), называется критерием согласия χ². Проверка нормальности распределения согласно критерию χ² сводится к следующему. 1. Данные наблюдений группируют по интервалам, как при построении гистограммы, и подсчитывают частоты mi. Если в некоторые интервалы попадает меньше пяти наблюдений, то такие интервалы объединяют с соседними. При этом число степеней свободы k, конечно, уменьшается. 2. Вычисляют среднее арифметическое 3. Для каждого интервала находят вероятности попадания в них результатов наблюдений либо по общей формуле (29), либо приближенно как произведение плотности теоретического распределения в середине интервала на его длину: 4. Для каждого интервала вычисляют величины χ²i(i=1,2,…,r) и суммируют их по всем i, в результате чего получают меру расхождения χ². 5. Определяют число степеней свободы k=r-3 и, задаваясь уровнем значимости q=1-a, находят по табл. П.6 приложения значения χ²k,0.5q и (χ²k,0.5q, χ²k,1-0.5q). Если χ²k,0.5q < χ²k < χ²k,1-0.5q, то распределение результатов наблюдений считают нормальным. Критерий согласия χ²k, построенный на предельном переходе при n→∞, рекомендуется применять, если общее число наблюдений больше сорока. При малом числе наблюдений 11<n<50 нормальность распределения результатов наблюдений проверяется с помощью двух критериев. Первый критерий основан на вычислении статистики Гипотеза о нормальности распределения на основании первого критерия принимается, если при данном числе наблюдений и выбранном уровне значимости q1 соблюдается условие где На основании второго критерия гипотеза о нормальности распределения принимается, если не более m разностей Φ(Z0.5(1+α))=0.5(1+α) Величина α находится при заданном уровне значимости q2 второго критерия по данным табл. П.9. Распределение результатов наблюдения считается отличным от нормального, если оно не соответствует хотя бы одному из этих двух критериев. Уровень значимости составного критерия q ≤ q1+q2. При малом числе наблюдений для оценки нормальности можно воспользоваться понятием статистической функции распределения результатов наблюдений. Для ее построения полученные в процессе эксперимента результаты группируют в так называемый вариационный ряд X*(1),X*(2),…,X*(n) члены которого располагаются в порядке их возрастания, так что всегда X*(1)≤X*(2)≤…≤X*(n). Статистическую функцию распределения Fn(xk) определяют по формуле Fn(xk) представляет собой ступенчатую линию, скачки которой соответствуют значениям членов вариационного ряда. Каждый скачок равен Если число наблюдений безгранично увеличивать, то статистическая функция распределения сходится по вероятности к истинной функции Fn(x). Для проверки нормальности распределения результатов наблюдений по табл.3 приложения находят значения zk, соответствующие полученным значениям Fn(xk) статистической функции распределения Φ(zk)=Fn(xk). Но переменная z определяется через результаты наблюдений как и если в координатах z, x нанести точки zk, xk, то при нормальном распределении они должны расположиться вдоль одной прямой линии. Если же в результате такого построения получится некоторая кривая линия, то гипотезу о нормальности распределения придется отвергнуть как противоречащую опытным данным. Пример. Даны результаты девятнадцати измерений длины детали (см. табл. 3). Проверить нормальность распределения результатов наблюдений. Вычисления по изложенной методике сведены в табл.8. Таблица 8
На рис. 12 представлена зависимость zk(xk). Отдельные точки располагаются очень близко к прямой, поэтому распределение результатов наблюдений можно считать нормальным. 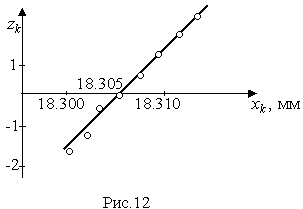 4.8. Обнаружение грубых погрешностей В начале главы уже было отмечено, что грубыми называют погрешности, явно превышающие по своему значению погрешности, оправданные условиями проведения эксперимента. Для их устранения желательно еще перед измерениями определить значение искомой величины приближенно, с тем чтобы в дальнейшем можно было сконцентрировать внимание лишь на уточнении предварительных данных. Если оператор в процессе измерений обнаруживает, что результат одного из наблюдений резко отличается от других, и находит причины этого, то он, конечно, вправе отбросить этот результат и провести повторные измерения. Но необдуманное отбрасывание резко отличающихся от других результатов может привести к существенному искажению характеристик рассеивания ряда измерений, поэтому повторные измерения лучше проводить не взамен сомнительных, а в дополнение к ним. Особенно остро ставится вопрос об устранении грубых погрешностей при обработке уже имеющегося материала, когда невозможно учесть все обстоятельства, при которых проводили измерения. В этом случае приходится прибегать к чисто статистическим методам. Вопрос о том, содержит ли данный результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что результат наблюдения Xi не содержит грубой погрешности, т.е. является одним из значений случайной величины Х с законом распределения FX(x), статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший Xmax или наименьший Xmin из результатов наблюдений. Поэтому для проверки гипотезы следует воспользоваться распределениями величин Функции их распределения определяют методами теории вероятностей [3]. Они совпадают между собой и для нормального распределения результатов наблюдений протабулированы и представлены в табл. П.7 приложения. По данным этой таблицы, при заданной доверительной вероятности α или уровне значимости q=1–α можно для количества измерения n=3–25 найти те наибольшие значения νa, которые случайная величина ν может еще принять по чисто случайным причинам. Если вычисленное по опытным данным значение ν окажется меньше νa, то гипотеза принимается; в противном случае ее следует отвергнуть как противоречащую данным наблюдений. Тогда результат Xmax или соответственно Xmin приходится рассматривать как содержащий грубую погрешность и не принимать его во внимание при дальнейшей обработке результатов наблюдений. Глава 5. СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
5.1. Классификация систематических погрешностей Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины [15, 17]. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалов, прогрессивная технология — все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться. В предыдущих параграфах, посвященных случайным погрешностям, было показано, что единственно правильным методом их анализа является математическая статистика. Случайные погрешности измерения изучались только в совокупности, без рассмотрения их фактических значений в каждом опыте. Систематические погрешности приходится изучать в каждом случае отдельно. Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру их проявления при измерениях. В зависимости от причин возникновения рассматриваются четыре вида систематических погрешностей: 1. Погрешности метода, или теоретические погрешности, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений. Погрешности метода возникают также при экстраполяции свойства, измеренного на ограниченной части некоторого объекта, на весь объект, если последний не обладает однородностью измеряемого свойства. Так, считая диаметр цилиндрического вала равным результату, полученному при измерении в одном сечении и в одном направлении, мы допускаем систематическую погрешность, полностью определяемую отклонениями формы исследуемого вала. При определении плотности вещества по измерениям массы и объема некоторой пробы возникает систематическая погрешность, если проба содержала некоторое количество примесей, а результат измерения принимается за характеристику данного вещества вообще. К погрешностям метода следует отнести также те погрешности, которые возникают вследствие влияния измерительной аппаратуры на измеряемые свойства объекта. Подобные явления возникают, например, при измерении длин, когда измерительное усилие используемых приборов достаточно велико, при регистрации быстропротекающих процессов недостаточно быстродействующей аппаратурой, при измерениях температур жидкостными или газовыми термометрами и так далее. 2. Инструментальные погрешности, зависящие от погрешностей применяемых средств измерений. Среди инструментальных погрешностей в отдельную группу выделяются погрешности схемы, не связанные с неточностью изготовления средств измерения и обязанные своим происхождением самой структурной схеме средств измерений. Исследование инструментальных погрешностей является предметом специальной дисциплины — теории точности измерительных устройств. 3. Погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, являющихся частью единого комплекса, несогласованностью их характеристик, влиянием внешних температурных, гравитационных, радиационных и других полей, нестабильностью источников питания, несогласованностью входных и выходных параметров электрических цепей приборов и так далее. 4. Личные погрешности, обусловленные индивидуальными особенностями наблюдателя. Такого рода погрешности вызываются, например, запаздыванием или опережением при регистрации сигнала, неправильным отсчетом десятых долей деления шкалы, асимметрией, возникающей при установке штриха посередине между двумя рисками. По характеру своего поведения в процессе измерения систематические погрешности подразделяются на постоянные и переменные. Постоянные систематические погрешности возникают, например, при неправильной установке начала отсчета, неправильной градуировке и юстировке средств измерения и остаются постоянными при всех повторных наблюдениях. Поэтому, если уж они возникли, их очень трудно обнаружить в результатах наблюдений. Среди переменных систематических погрешностей принято выделять прогрессивные и периодические. Прогрессивная погрешность возникает, например, при взвешивании, когда одно из коромысел весов находится ближе к источнику тепла, чем другое, поэтому быстрее нагревается и удлиняется. Это приводит к систематическому сдвигу начала отсчета и к монотонному изменению показаний весов. Периодическая погрешность присуща измерительным приборам с круговой шкалой, если ось вращения указателя не совпадает с осью шкалы. Все остальные виды систематических погрешностей принято называть погрешностями, изменяющимися по сложному закону. В тех случаях, когда при создании средств измерений, необходимых для данной измерительной установки, не удается устранить влияние систематических погрешностей, приходится специально организовывать измерительный процесс и осуществлять математическую обработку результатов. Методы борьбы с систематическими погрешностями заключаются в их обнаружении и последующем исключении путем полной или частичной компенсации. Основные трудности, часто непреодолимые, состоят именно в обнаружении систематических погрешностей, поэтому иногда приходится довольствоваться приближенным их анализом. 5.2. Способы обнаружения систематических погрешностей Результаты наблюдений, полученные при наличии систематических погрешностей, будем называть неисправленными и в отличие от исправленных снабжать штрихами их обозначения (например X'1, X'2 и т.д.). Вычисленные в этих условиях средние арифметические значения и отклонения от результатов наблюдений будем также называть неисправленными и ставить штрихи у символов этих величин. Таким образом, Поскольку неисправленные результаты наблюдений включают в себя систематические погрешности, сумму которых для каждого i-го наблюдения будем обозначать через θi, то их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на некоторую величину θ, называемую систематической погрешностью неисправленного среднего арифметического. Действительно, Если систематические погрешности постоянны, т.е. θi=θ, i=1,2,…n, то неисправленные отклонения могут быть непосредственно использованы для оценки рассеивания ряда наблюдений. В противном случае необходимо предварительно исправить отдельные результаты измерений, введя в них так называемые поправки, равные систематическим погрешностям по величине и обратные им по знаку: q = –θi. Таким образом, для нахождения исправленного среднего арифметического и оценки его рассеивания относительно истинного значения измеряемой величины необходимо обнаружить систематические погрешности и исключить их путем введения поправок или соответствующей каждому конкретному случаю организации самого измерения. Остановимся подробнее на некоторых способах обнаружения систематических погрешностей. Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от средних арифметических, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основании некоторых априорных знаний об этих погрешностях, получаемых, например, при поверке средств измерений. Измеряемая величина при поверке обычно воспроизводится образцовой мерой, действительное значение которой известно. Поэтому разность между средним арифметическим результатов наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения, равна искомой систематической погрешности. Ценность полученных при поверке результатов определяется их постоянством в течение некоторого промежутка времени и независимостью от тех изменений внешних условий, которые допустимы при эксплуатации средств измерений с заданной точностью. Тогда полученные при поверке данные могут быть использованы для вычисления поправок, необходимых для исправления результатов наблюдений. Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических. Вначале рассмотрим случай, когда в ряде результатов наблюдений предполагается наличие постоянной систематической погрешности. Для того чтобы удостовериться в этом, исследователь, сделав несколько измерений, заменяет некоторые меры или измерительные приборы, включенные в установку и являющиеся предполагаемыми источниками постоянных систематических погрешностей, другими мерами и измерительными приборами и проводит еще несколько измерений. Рассматриваемый способ обнаружения постоянных систематических погрешностей можно сформулировать следующим образом: если неисправленные отклонения результатов наблюдений резко изменяются при изменении условий наблюдений, то данные результаты содержат постоянную систематическую погрешность, зависящую от условий наблюдений. При прогрессивной систематической погрешности последовательность неисправленных отклонений результатов наблюдений обнаруживает тенденцию к возрастанию или убыванию. На рис. 13 изображена зависимость погрешности измерения от длины измеряемой детали.  Несмотря на большие случайные изменения погрешности тенденция к увеличению ее в отрицательном направлении с ростом измеряемой величины явно обнаруживается. Если бы случайные погрешности были невелики, то значения неисправленных отклонений меняли бы свой знак при некотором среднем значении измеряемой величины. Случайные погрешности несколько искажают эту картину, однако, если они даже одного порядка малости с систематическими погрешностями, в последовательности знаков можно заметить некоторую неравномерность: неисправленные отклонения результатов одного знака чаще встречаются в отрицательной полуплоскости, чем в положительной. Если же в ряде результатов наблюдений присутствует периодическая систематическая погрешность, то группы знаков плюс и минус в последовательности неисправленных отклонений результатов наблюдений могут периодически сменять друг друга, если, конечно, случайные погрешности не особенно велики. Обобщая два рассмотренных случая, можно сказать: если последовательность знаков плюс сменяется последовательностью знаков минус или наоборот, то данный ряд результатов наблюдений обнаруживает прогрессивную погрешность, если группы знаков плюс и минус чередуются — периодическую погрешность. 5.3. Введение поправок. Неисключенная систематическая погрешность Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерений. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдении, которые позволяют оценить степень рассеивания результатов. Для исправления результатов наблюдений их складывают с поправками, равными систематическим погрешностям по величине и обратными им по знаку. Поправку определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью. Для исправления результата наблюдения его складывают только со средним арифметическим значением поправки: Xi = Xi'+q, (59) где Xi и Xi' — соответственно исправленный и неисправленный результаты наблюдений, q — среднее арифметическое значение поправки, определяемые экспериментально. Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая. Например, при измерениях и поверках с помощью образцовых манометров следует вводить поправки к их показаниям на местное значение ускорения свободного падения где P — измеряемое давление. Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок. При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается. Действительно, при исправлении неисправленного результата Xi' путем введения поправок qi±sj, j=1,2,…,m по формуле дисперсия s²x становится равной где s²x — оценка дисперсии неисправленных результатов; s²x' — оценка дисперсии j-й поправки. Поправку имеет смысл вводить до тех пор, пока она уменьшает доверительные границы погрешности, т.е. пока выполняется неравенство При малой дисперсии поправки на основании формулы (62) может показаться, что введение любой поправки повышает достоверность результата. Однако следует помнить, что погрешность результата выражается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц разряда, следующего за последним десятичным знаком погрешности результата, будет все равно потеряна при округлении, и вводить ее не имеет смысла. Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности. К их числу относятся: • погрешности определения поправок; • погрешности, зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок; • погрешности, связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.). Перечисленные погрешности малы и поправки на них не вводятся. Для каждого данного измерения элементарные составляющие систематической погрешности имеют вполне определенные значения, но эти значения нам неизвестны. Известно лишь, что в массе однотипных измерений эти составляющие лежат в определенных границах где m1— число равномерно распределенных и m2 — число нормально распределенных элементарных составляющих. Глава 6. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ИСПРАВЛЕННЫХ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
6.1. Обработка результатов прямых равнорассеянных наблюдений Прямыми называются измерения, в результате которых искомое значение физической величины находят непосредственно из опытных данных. Прямые измерения осуществляются путем многократных наблюдений. Результаты наблюдений X1,X2,…,Xn называются равнорассеянными, если они являются независимыми, одинаково распределенными случайными величинами. Равнорассеянные результаты получают при измерениях, проводимых одним наблюдателем или группой наблюдателей с помощью одних и тех же методов и средств измерений в неизменных условиях внешней среды. Обработка результатов наблюдений в соответствии с методикой прямых измерений с многократными наблюдениями производится в следующем порядке: 1. Путем введения поправок исключают известные систематические погрешности из результатов наблюдений. 2. Вычисляют среднее арифметическое 3. Вычисляют оценку sx среднеквадратического отклонения результатов наблюдения и оценку 4. Проверяют гипотезу о нормальности распределения результатов наблюдения. Если число результатов n>50, используют критерий Пирсона χ², при 15<n<50 — составной критерий. Уровень значимости выбирается из интервала 0.02–0.10. При n<15 нормальность распределения не проверяется. 5. Если результаты наблюдений распределены нормально, то определяют наличие грубых погрешностей и промахов и если последние обнаружены, соответствующие результаты отбраковывают и повторяют вычисления. 6. Вычисляют доверительные границы случайной погрешности при доверительной вероятности P=0.95, а также при P=0.99, если измерения в дальнейшем повторить нельзя. 7. Определяют границы неисключенной систематической погрешности результата измерений. В качестве составляющих неисключенной систематической погрешности рассматривают погрешности метода, погрешности средств измерений (например пределы допускаемой основной и дополнительных погрешностей, если их случайные составляющие пренебрежимо малы) и погрешности, вызванные другими источниками. При суммировании составляющих неисключенные систематические погрешности средств измерений рассматриваются как случайные величины. Если их распределение неизвестно, то принимается равномерное распределение и тогда границы неисключенной систематической погрешности результата при числе составляющих m>4 определяют как где θi — границы отдельных составляющих общим числом m; k — коэффициент, равный 1.1 при доверительной вероятности P=0.95 и 1.4 при P=0.99. 8. Вычисляют доверительные границы погрешности результата. Если выполняется условие Если эти условия не выполняются, то доверительные границы погрешности результата определяют по формуле Δ=K*sΣ, где коэффициент K находят из выражения а среднеквадратическое общей погрешности результата 9. Результат измерения записывают в виде Если полученный при измерениях результат в дальнейшем используется для анализа и сопоставления с другими результатами или является промежуточным для нахождения других величин, то необходимо указать раздельно границы систематической погрешности и среднеквадратическое отклонение случайной погрешности: В некоторых случаях нас может интересовать не сама измеряемая величина, а связанная с ней функциональной зависимостью. Требуется найти интервальную или точечную оценку ее истинного значения. Решается такая задача следующим образом. Пусть При проведении точных измерений Пример. Измеренный диаметр круга d=94.75±0.05 мм. Требуется найти площадь круга По формуле (66) 6.2. Обработка неравнорассеянных рядов наблюдений В практике исследовательских работ часто встречаются ситуации, когда необходимо найти наиболее достоверное значение величины и оценить его возможные отклонения от истинного значения на основании измерений, проводимых разными наблюдателями с применением разнообразных измерительных средств и методов измерений в различных лабораториях или условиях внешней среды. Ряды получающихся при этом результатов наблюдений называются неравнорассеянными, если оценки их дисперсий значительно отличаются друг от друга, а средние арифметические являются оценками одного и того же значения измеряемой величины. Если средние неравнорассеянных рядов наблюдений мало отличаются друг от друга, то говорят о высокой воспроизводимости измерений, которая количественно характеризуется параметрами рассеивания результатов. Рассмотрим некоторые случаи, приводящие к необходимости обработки результатов неравнорассеянных измерений: 1. Если при точных измерениях необходимо убедиться в отсутствии неисключенных систематических погрешностей, то измерения проводятся несколькими исследователями или группами исследователей. Если средние арифметические полученных рядов наблюдений незначительно отличаются друг от друга и ничто не указывает на наличие систематических погрешностей, то заманчиво объединить все полученные результаты и на основе их математической обработки получить более достоверные сведения об измеряемой величине. 2. Аналогичные измерения были выполнены в разных лабораториях различными методами и получены отличающиеся друг от друга результаты. Естественно и в этом случае, используя все имеющиеся данные, попытаться получить более достоверные значения измеряемых величин. 3. Измерения, относящиеся к образцовым мерам и измерительным приборам, часто повторяются через некоторое время. В конце концов накапливаются ряды наблюдений и возникает необходимость объединить их. Точность рядов наблюдений различна, с одной стороны, из-за того, что для впервые проводимых измерений характерно большее рассеивание результатов, а с другой стороны, из-за того, что с течением времени средства измерения стареют или заменяются новыми. Во всех описанных ситуациях приходится прибегать к методам обработки результатов неравнорассеянных рядов наблюдений, задача которых в общем случае заключается в нахождении наиболее достоверного значения измеряемой величины и оценки воспроизводимости измерений. Основой для расчета служат следующие данные: • • σ1,σ2,…,σm — среднеквадратические отклонения (или их оценки) результатов наблюдений в отдельных рядах; • n1,n2,…,nm — числа наблюдений в каждом ряду; • m — число рядов. Если результаты наблюдений во всех рядах распределены нормально, то нормально распределены и все m средних арифметических Q – истинное значение измеряемой величины (при условии, что систематические погрешности исключены). Для практической обработки результатов неравнорассеянных рядов наблюдений необходимо ввести параметр вес отдельных средних арифметических: Веса характеризуют степень нашего доверия к соответствующим рядам наблюдений. Чем больше число наблюдений в каждом данном ряду и чем меньше дисперсия результатов наблюдений, тем больше степень доверия к полученному при этом среднему арифметическому и с тем большим весом оно будет учтено при определении оценки истинного значения измеряемой величины Иногда удобно пользоваться безразмерными весовыми коэффициентами тогда выражение для среднего взвешенного приобретает простой вид В соответствии со свойствами оценок максимального правдоподобия дисперсия среднего взвешенного должна равняться единице, деленной на математическое ожидание второй производной от логарифмической функции правдоподобия: Отсюда следует, что дисперсия среднего взвешенного меньше дисперсии любого из исходных средних арифметических отдельных рядов наблюдений и поэтому при обработке неравнорассеянных рядов наблюдений точность измерений повышается. Если теоретические дисперсии При малом числе нормально распределенных результатов наблюдений пользуются распределением Стьюдента с числом степеней свободы Если же об исходных распределениях нет никаких заслуживающих внимания данных, то на основании центральной предельной теоремы можно все-таки предполагать, что распределение среднего взвешенного нормально, поскольку оно является суммой большого числа случайных величин с конечными дисперсиями и математическими ожиданиями. Пример. Тремя коллективами экспериментаторов с помощью различных методов измерения были получены следующие значения ускорения свободного падения (со среднеквадратическими отклонениями результатов измерений): g=(981.9190±0.0004) смˉ²; g=(981.9215±0.0016) смˉ²; g=(981.9230±0.0020) смˉ²; Весовые коэффициенты отдельных результатов вычислим по формуле (68): Среднее взвешенное в соответствии с уравнением (69) составляет: и его дисперсия (70) 6.3. Обработка результатов косвенных измерений При косвенных измерениях значение искомой величины получают на основании известной зависимости, связывающей ее с другими величинами, подвергаемыми прямым измерениям. Вначале рассмотрим тот простейший случай, когда искомая величина QZ определяется как сумма двух величин QX и QY: QZ = QX + QY (72) Поскольку результаты прямых измерений величин QX и QY (после исключения систематических погрешностей) включают в себя некоторые случайные погрешности, то формулу косвенного измерения суммы можно переписать в виде где Из уравнения (73) непосредственно вытекает справедливость двух следующих равенств: т.е. оценкой истинного значения косвенно измеряемой величины должна служить сумма оценок истинных значений исходных величин, случайные погрешности которых складываются. Математическое ожидание оценки а ее дисперсия: Входящее в это выражение математическое ожидание произведения случайных погрешностей называется корреляционным моментом и определяет степень “тесноты” линейной зависимости между погрешностями. Вместо корреляционного момента часто пользуются безразмерной величиной, называемой коэффициентом корреляции: Отсюда, в частности, следует, что коэффициент корреляции между погрешностями λX и λY средних арифметических равен коэффициенту корреляции между погрешностями δX и δY результатов отдельных измерений величин QX и QY: С учетом коэффициента корреляции дисперсия результата косвенных измерений, т. е. оценки истинного значения косвенно измеряемой величины, Если погрешности измерения величин QX и QY не коррелированы, то выражение (76) упрощается: В тех случаях, когда теоретические дисперсии распределения результатов прямых измерений неизвестны, определяется оценка Оценки коэффициента корреляции m = min(nX, nY) — наименьшее из чисел наблюдений nX и nY. При положительной корреляции, т. е. когда rXY > 0, одна из погрешностей имеет тенденцию возрастать при увеличении другой, если же корреляция отрицательна, то rXY < 0 и погрешность измерения одной величины обнаруживает тенденцию к уменьшению при увеличении погрешности измерения другой величины. Возможные значения коэффициента корреляции лежат в интервале –1 < rXY < +1. Если rXY = 0, то погрешности измерения некоррелированы. О наличии корреляции удобно судить по графику, на котором в координатах X, Y изображены пары последовательно получаемых результатов измерения величин QX и QY. На рис.14 изображены случаи совместного распределения результатов измерения при положительной (рис. 14, а) и отрицательной (рис. 14, б) корреляции. Результаты измерений на рис. 15, в некоррелированы. 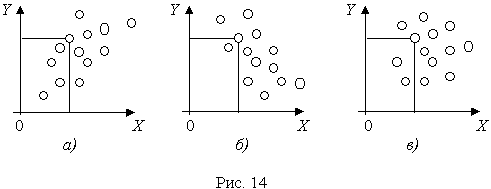 Чаще всего наличия корреляции следует ожидать в тех случаях, когда обе величины измеряются одновременно однотипными измерительными средствами, причем неуловимые изменения внешних воздействий (электрических, магнитных, температурных и других полей, условий питания) одновременно заметно влияют на формирование случайных погрешностей их измерения. В некоторых случаях причиной корреляции между результатами измерений может стать сам оператор, поскольку при некоторых исследованиях, связанных с ручным уравновешиванием приборов сравнения (сличением мер на точных весах, в фотометрии), искусство и опыт наблюдателя оказывают значительное влияние на результаты измерений. В тех же случаях, когда исходные величины измеряют с помощью различных средств измерения в разное время, можно с полным правом ожидать, что результаты, если и будут коррелированы, то очень мало, и коэффициентом корреляции в выражениях (76) и (78) можно пренебречь. Распределение результата косвенных измерений будет нормальным, если нормальны распределения результатов прямых измерений. В этих условиях для построения доверительного интервала, накрывающего истинное значение измеряемой величины, следует применить нормированную функцию нормального распределения, если число измерений достаточно велико. Если же объемы рядов прямых измерений недостаточно велики, то можно воспользоваться распределением Стьюдента с некоторым “эффективным” числом степеней свободы, которое для рассматриваемого случая при независимости погрешностей измерения (rXY = 0) подсчитывается по формуле где nX и nY — числа прямых наблюдений величин QX и QY. Если числа наблюдений одинаковы (nX = nY = n), то выражение для эффективного числа степеней свободы распределения Стьюдента упрощается: Итоговый результат измерений записываем в виде: где tp определяется из выражения: или Рассмотренные выражения можно использовать и в том случае, когда искомая величина является суммой от измеряемых прямыми способами величин: К такой формуле приходим при измерении больших величин по частям, например при измерении длин с помощью концевых мер длины, взвешивании с применением набора гирь, измерении на электрических приборах сравнения с помощью магазинов сопротивлений, емкостей или индуктивностей, измерении объемов жидкостей мерниками меньшей вместимости и так далее. В этих случаях в качестве наиболее достоверной оценки Пример. Без учета поправки на теплообмен подъем температуры Δt в калориметре определяют как разность между конечной t2 и начальной t1 температурами. После обработки опытных данных были получены следующие (округленные) результаты с соответствующими среднеквадратическими отклонениями: t1 = 25.10718°C, si = 0.6·10-4°C, t2 = 25.10739°C, si = 0.3·10-4°C. Результат косвенного измерения находим по формуле (74) как разность соответствующих средних арифметических: а среднеквадратическое отклонение результата по формуле (77): Итог измерения: Δt = (2.00021±0.00007)°C, P=0.6826. Здесь мы приняли tp = 1, что при нормальном распределении погрешностей измерений и достаточно большом числе их наблюдений соответствует доверительной вероятности 0.6826 нахождения подъема температуры в указанных пределах. 6.4. Критерии ничтожных погрешностей Не все частные погрешности Ek косвенного измерения играют одинаковую роль в формировании итоговой погрешности результата. Так, например, если частные погрешности удовлетворяют неравенству то ими можно пренебречь. Эта формула в метрологии называется критерием ничтожных погрешностей, а сами погрешности, отвечающие условию (78), называются ничтожными или ничтожно малыми. Использование критерия ничтожных погрешностей при решении задачи косвенных измерений позволяет найти те величины, повышение точности измерения которых позволит уменьшить суммарную погрешность результата. Очевидно, не имеет смысла повышать точность измерения тех величин, частные погрешности которых и без того ничтожно малы. Глава 7. СРЕДСТВА ИЗМЕРЕНИЙ. ПОГРЕШНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ
7.1. Метрологические характеристики средств измерений Все средства измерений, независимо от их конкретного исполнения, обладают рядом общих свойств, необходимых для выполнения ими их функционального назначения. Технические характеристики, описывающие эти свойства и оказывающие влияние на результаты и на погрешности измерений, называются метрологическими характеристиками [9, 10]. Перечень важнейших из них регламентируется ГОСТ “Нормируемые метрологические характеристики средств измерений”. Комплекс нормируемых метрологических характеристик устанавливается таким образом, чтобы с их помощью можно было оценить погрешность измерений, осуществляемых в известных рабочих условиях эксплуатации посредством отдельных средств измерений или совокупности средств измерений, например автоматических измерительных систем. Одной из основных метрологических характеристик измерительных преобразователей является статическая характеристика преобразования (иначе называемая функцией преобразования или градуировочной характеристикой). Она устанавливает зависимость y=f(x) информативного параметра у выходного сигнала измерительного преобразователя от информативного параметра х входного сигнала. Статическая характеристика нормируется путем задания в форме уравнения, графика или таблицы. Понятие статической характеристики применимо и к измерительным приборам, если под независимой переменной х понимать значение измеряемой величины или информативного параметра входного сигнала, а под зависимой величиной – показание прибора. Если статическая характеристика преобразования линейна, т.е. y=Kx, то коэффициент K называется чувствительностью измерительного прибора (преобразователя). В противном случае под чувствительностью следует понимать производную от статической характеристики. Важной характеристикой шкальных измерительных приборов является цена деления, т.е. то изменение измеряемой величины, которому соответствует перемещение указателя на одно деление шкалы. Если чувствительность постоянна в каждой точке диапазона измерения, то шкала называется равномерной. При неравномерной шкале нормируется наименьшая цена деления шкалы измерительных приборов. У цифровых приборов шкалы в явном виде нет, и на них вместо цены деления указывается цена единицы младшего разряда числа в показании прибора. Важнейшей метрологической характеристикой средств измерений является погрешность. Под абсолютной погрешностью меры понимается алгебраическая разность между ее номинальным Xн и действительным Xд значениями: Δ = Xн – Xд (84) а под абсолютной погрешностью измерительного прибора — разность между его показанием Xп и действительным значением Xд измеряемой величины: Δ = Xп – Xд (85) Абсолютная погрешность измерительного преобразователя может быть выражена в единицах входной или выходной величины. В единицах входной величины абсолютная погрешность преобразователя определяется как разность между значением входной величины X, найденной по действительному значению выходной величины и номинальной статической характеристике преобразователя, и действительным значением Xд входной величины: Δ = X – Xд Однако в большей степени точность средства измерений характеризует относительная погрешность, т.е. выраженное в процентах отношение абсолютной погрешности к действительному значению измеряемой или воспроизводимой данным средством измерений величины: Обычно δ ≪ 1, поэтому в формулу (86) вместо действительного значения часто может быть подставлено номинальное значение меры или показание измерительного прибора. Если диапазон измерения прибора охватывает и нулевое значение измеряемой величины, то относительная погрешность обращается в бесконечность в соответствующей ему точке шкалы. В этом случае пользуются понятием приведенной погрешности, равной отношению абсолютной погрешности измерительного прибора к некоторому нормирующему значению XN: В качестве нормирующего значения принимается значение, характерное для данного вида измерительного прибора. Это может быть, например, диапазон измерений, верхний предел измерений, длина шкалы и т.д. Погрешности измерительных средств принято подразделять на статические, имеющие место при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей, и динамические, появляющиеся при измерении переменных величин и обусловленные инерционными свойствами средств измерений. Согласно общей классификации, статические погрешности измерительных средств делятся на систематические и случайные. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности находят при поверке и аттестации образцовых приборов, например, измерением наперед заданных значений измеряемой величины в нескольких точках шкалы. В результате строится кривая или создается таблица погрешностей, которая используется для определения поправок. Поправка в каждой точке шкалы численно равна систематической погрешности и обратна ей по знаку, поэтому при определении действительного значения измеряемой величины поправку следует прибавить к показанию прибора. Так, если поправка к показанию динамометра 120 Н равна +0.6 Н, то действительное значение измеряемой силы составляет 120+0.6=120.6 Н. Удобнее пользоваться поправкой, чем систематической погрешностью, поэтому приборы чаще снабжают кривыми или таблицами поправок. Систематическую погрешность в функции измеряемой величины можно представить в виде суммы погрешности схемы, определяемой самой структурной схемой средства измерений, и технологических погрешностей, обусловленных погрешностями изготовления его элементов. Как те, так и другие виды погрешностей можно рассматривать в качестве систематических лишь при измерении постоянной величины с помощью одного экземпляра измерительного прибора. В массе же измерений различных значений физической величины, осуществляемых одним или многими приборами того же типоразмера, эти систематические погрешности приходится относить к классу случайных. Между погрешностями схемы и технологическими погрешностями средств измерений существует принципиальная разница. Если первые накладывают свой отпечаток на характер изменения по шкале суммарной погрешности всех средств измерений данного типоразмера, то технологические погрешности индивидуальны для каждого экземпляра, т. е. их значения в одних и тех же точках шкалы различны для различных экземпляров приборов. На рис. 15, а показано взаимное положение статических характеристик реального f(Q) и идеального f0(Q) приборов при наличии только погрешностей схемы. Технологические погрешности в большой степени искажают эту картину. Результатом их проявления является: а) поступательное смещение статической характеристики относительно характеристики идеального прибора и возникновение погрешности, постоянной в каждой точке шкалы; эта погрешность называется аддитивной (рис. 15, б); б) поворот статической характеристики и появление погрешности, линейно возрастающей или убывающей с ростом измеряемой величины и называемой мультипликативной погрешностью (рис. 15, в); в) нелинейные искажения статической характеристики (рис. 15, г); г) появление погрешности обратного хода, выражающейся в несовпадении статических характеристик прибора при увеличении и уменьшении измеряемой величины (рис. 15, д). 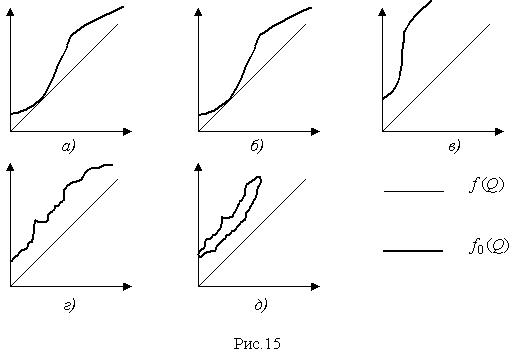 Динамические погрешности обусловливаются инерционными свойствами средств измерений и появляются при измерении переменных во времени величин. Типичным случаем является измерение с регистрацией сигнала, изменяющегося со временем. Если x(t) и y(t) — сигналы на входе и на выходе средства измерений с чувствительностью K, то динамическая погрешность Для средств измерений, являющихся линейными динамическими системами с постоянными во времени параметрами, наиболее общая характеристика динамических свойств — это дифференциальное уравнение. В этом случае уравнение линейное с постоянными коэффициентами: где y(i)(t) и x(j)(t) — i-e и j-e производные входного и выходного сигналов; ai и bj — постоянные коэффициенты, n и m – порядок левой и правой частей уравнения, причем n < m. Дифференциальное уравнение является метрологической характеристикой средств измерения, поскольку позволяет при известном сигнале на входе x(t) найти выходной сигнал y(t) и после подстановки их в выражение (83) вычислить динамическую погрешность. Для нормирования динамических свойств средств измерения часто указывают на дифференциальное уравнение, а другие, производные от него динамические характеристики, находятся экспериментальным путем. Сюда относятся передаточная функция, амплитудная и фазовая частотные характеристики, переходная и импульсная переходная функции. К числу метрологических характеристик средств измерения относятся и неинформативные параметры выходного сигнала измерительного преобразователя, поскольку они могут оказывать существенное влияние на погрешность средства измерений. Например, непостоянство амплитуды колебаний баланса наручных часов (неинформативный параметр) приводит к изменению частоты его колебаний (информативный параметр). При восприятии измеряемой величины или измерительного сигнала средство измерений оказывает некоторое воздействие на объект измерения или на источник сигнала. Результатом этого воздействия может быть некоторое изменение измеряемой величины относительно того значения, которое имело место при отсутствии средства измерений. Такое обратное воздействие средства измерений на объект измерений особенно четко просматривается при измерении электрических величин. Так, ЭДС нормального элемента определяется как напряжение на его зажимах в режиме холостого хода. При измерении этого напряжения вольтметром с некоторым конечным входным сопротивлением результат измерения будет зависеть от соотношения между внутренним сопротивлением нормального элемента (его выходное сопротивление) и входным сопротивлением вольтметра. Для оценки возникающей при этом погрешности необходимо знать значения этих сопротивлений, поэтому их следует рассматривать как метрологические характеристики. Влияние внешних воздействий и неинформативных параметров сигналов (влияющих величин) описывается с помощью метрологических характеристик, называемых функциями влияния. Функция влияния Ψ(ξ1,ξ2,…ξq) — это зависимость соответствующей метрологической характеристики из числа вышеперечисленных от влияющих величин ξ1,ξ2,…ξq (температуры внешней среды, параметров внешних вибраций и т.д.). В большинстве случаев можно ограничиться набором функций влияния каждой из влияющих величин Ψ(ξ1),Ψ(ξ2),…,Ψ(ξq), но иногда приходится использовать функции совместного влияния нескольких величин, если изменение одной из влияющих величин приводит к изменению функции влияния другой. 7.2. Нормирование метрологических характеристик средств измерений Под нормированием понимается установление границ на допустимые отклонения реальных метрологических характеристик средств измерений от их номинальных значений. Только посредством нормирования метрологических характеристик можно добиться их взаимозаменяемости и обеспечить единство измерений в государстве. Реальные значения метрологических характеристик определяют при изготовлении средств измерений и затем проверяют периодически во время эксплуатации. Если при этом хотя бы одна из метрологических характеристик выходит за установленные границы, то такое средство измерений либо подвергают регулировке, либо изымают из обращения [11]. Нормы на значения метрологических характеристик устанавливаются стандартами на отдельные виды средств измерения. При этом делается различие между нормальными и рабочими условиями применения средств измерения. Нормальными считаются такие условия применения средств измерений, при которых влияющие на процесс измерения величины (температура, влажность, частота, напряжение питания, внешние магнитные поля и т.д.), а также неинформативные параметры входных и выходных сигналов находятся в нормальной для данных средств измерений области значений, т.е. в такой области, где их влиянием на метрологические характеристики можно пренебречь. Нормальные области значений влияющих величин указываются в стандартах или технических условиях на средства измерений данного вида в форме номиналов с нормированными отклонениями, например, температура должна составлять 20±2°C, напряжение питания – 220 В±10% или в форме интервалов значений (влажность 30–80%). Рабочая область значений влияющих величин шире нормальной области значений. В ее пределах метрологические характеристики существенно зависят от влияющих величин, однако их изменения нормируются стандартами на средства измерений в форме функций влияния или наибольших допустимых изменений. За пределами рабочей области метрологические характеристики принимают неопределенные значения. Для нормальных условий эксплуатации средств измерений должны нормироваться характеристики суммарной погрешности и ее систематической и случайной составляющих. Суммарная погрешность Δ средств измерений в нормальных условиях эксплуатации называется основной погрешностью и нормируется заданием предела допускаемого значения Δд, т.е. того наибольшего значения, при котором средство измерений еще может быть признано годным к применению. Перечисленные выше метрологические характеристики следует нормировать не только для нормальной, но и для всей рабочей области эксплуатации средств измерений, если их колебания, вызванные изменениями внешних влияющих величин и неинформативных параметров входного сигнала в пределах рабочей области, существенно меньше номинальных значений. В противном случае эти характеристики нормируются только для нормальной области, а в рабочей области нормируются дополнительные погрешности путем задания функций влияния Ψ(ξ) или наибольших допустимых изменений Δl(ξ) раздельно для каждого влияющего фактора; в случае необходимости — и для совместного изменения нескольких факторов. Функции влияния нормируются формулой, числом, таблицей или задаются в виде номинальной функции влияния и предела допускаемых отклонений от нее. Для используемых по отдельности средств измерений, точность которых заведомо превышает требуемую точность измерений, нормируются только пределы Δд допускаемого значения суммарной погрешности и наибольшие допустимые изменения метрологических характеристик. Если же точность средств измерений соизмерима с требуемой точностью измерений, то необходимо нормировать раздельно характеристики систематической и случайной погрешности и функции влияния. Только с их помощью можно найти суммарную погрешность в рабочих условиях применения средств измерений. Динамические характеристики нормируются путем задания номинального дифференциального уравнения или передаточной, переходной, импульсной весовой функции. Одновременно нормируются наибольшие допустимые отклонения динамических характеристик от номинальных. 7.3. Классы точности средств измерений Класс точности — это обобщенная характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений. Классы точности регламентируются стандартами на отдельные виды средств измерения с использованием метрологических характеристик и способов их нормирования, изложенных в предыдущих главах. Стандарт не распространяется на средства измерений, для которых предусматриваются раздельные нормы на систематическую и случайные составляющие, а также на средства измерений, для которых нормированы номинальные функции влияния, а измерения проводятся без введения поправок на влияющие величины. Классы точности не устанавливаются и на средства измерений, для которых существенное значение имеет динамическая погрешность. Для остальных средств измерений обозначение классов точности вводится в зависимости от способов задания пределов допускаемой основной погрешности. Пределы допускаемой абсолютной основной погрешности могут задаваться либо в виде одночленной формулы Δ = ±a (90) либо в виде двухчленной формулы Δ = ±(a + bx) (91) где Δ и x выражаются одновременно либо в единицах измеряемой величины, либо в делениях шкалы измерительного прибора. Более предпочтительным является задание пределов допускаемых погрешностей в форме приведенной или относительной погрешности. Пределы допускаемой приведенной основной погрешности нормируются в виде одночленной формулы где число p = 1·10n, 1.5·10n, 2·10n, 2.5·10n, 4·10n, 5·10n, 6·10n (n = 1, 0, -1, -2…). Пределы допускаемой относительной основной погрешности могут нормироваться либо одночленной формулой либо двухчленной формулой где Xk — конечное значение диапазона измерений или диапазона значений воспроизводимой многозначной мерой величины, а постоянные числа q, c и d выбираются из того же ряда, что и число p. В обоснованных случаях пределы допускаемой абсолютной или относительной погрешности можно нормировать по более сложным формулам или даже в форме графиков или таблиц. Средствам измерений, пределы допускаемой основной погрешности которых задаются относительной погрешностью по одночленной формуле (93), присваивают классы точности, выбираемые из ряда чисел р и равные соответствующим пределам в процентах. Так для средства измерений с δ = 0.002 класс точности обозначается Если пределы допускаемой основной относительной погрешности выражаются двухчленной формулой (94), то класс точности обозначается как c/d, где числа с и d выбираются из того же ряда, что и p, но записываются в процентах. Так, измерительный прибор класса точности 0.02/0.01 характеризуется пределами допускаемой основной относительной погрешности Классы точности средств измерений, для которых пределы допускаемой основной приведенной погрешности нормируются по формуле (92), обозначаются одной цифрой, выбираемой из ряда для чисел p и выраженной в процентах. Если, например, γ=±0.005=±0.5%, то класс точности обозначается как 0.5 (без кружка). Классы точности обозначаются римскими цифрами или буквами латинского алфавита для средств измерений, пределы допускаемой погрешности которых задаются в форме графиков, таблиц или сложных функций входной, измеряемой или воспроизводимой величины. К буквам при этом допускается присоединять индексы в виде арабской цифры. Чем меньше пределы допускаемой погрешности, тем ближе к началу алфавита должна быть буква и тем меньше цифра. Недостатком такого обозначения класса точности является его чисто условный характер. В заключение данного раздела следует отметить, что никакое нормирование погрешностей средств измерений само по себе не может обеспечить единства измерений. Для достижения единства измерений необходима регламентация самих методик проведения измерений. 7.4. Регулировка и градуировка средств измерений Используя методы теории точности, всегда можно найти такие допуски на параметры элементов измерительного прибора, соблюдение которых гарантировало бы и без регулировки получение их с погрешностями, меньшими допустимых пределов. Однако во многих случаях эти допуски оказываются настолько малы, что изготовление прибора с заданными пределами допускаемых погрешностей становится технологически неосуществимым. Выйти из положения можно двумя путями: во-первых, расширить допуски на параметры некоторых элементов приборов и ввести в его конструкцию дополнительные регулировочные узлы, способные компенсировать влияние отклонений этих параметров от их номинальных значений, а во-вторых, осуществить специальную градуировку измерительного прибора. В большинстве случаев в измерительном приборе можно найти или предусмотреть такие элементы, вариация параметров которых наиболее заметно сказывается на его систематической погрешности, главным образом погрешности схемы, аддитивной и мультипликативной погрешностях. В общем случае в конструкции измерительного прибора должны быть предусмотрены два регулировочных узла: регулировка нуля и регулировка чувствительности. Регулировкой нуля уменьшают влияние аддитивной погрешности, постоянной для каждой точки шкалы, а регулировкой чувствительности уменьшают мультипликативные погрешности, меняющиеся линейно с изменением измеряемой величины. При правильной регулировке нуля и чувствительности уменьшается влияние погрешности схемы прибора. Кроме того, некоторые приборы снабжаются устройствами для регулировки погрешности схемы. После регулировки нуля, т.е. устранения аддитивной погрешности, систематическая погрешность обращается в нуль на нижнем пределе измерения, а в диапазоне измерения принимает значения, являющиеся случайной функцией Δc(X) измеряемой величины. Более высокими метрологическими характеристиками обладают измерительные приборы, имеющие узел регулировки чувствительности. Наличие такой регулировки позволяет поворачивать статическую характеристику, что открывает большие возможности для снижения погрешности схемы и, главным образом, мультипликативной погрешности. Так, одновременной регулировкой нуля и чувствительности можно свести систематическую погрешность к нулю сразу в нескольких точках шкалы прибора. От правильности выбора таких точек зависят значения оставшихся после регулировки систематических погрешностей в других точках шкалы. Теория регулировки должна дать ответ на вопрос, какие точки шкалы следует выбрать в качестве точек регулировки. Однако общего решения этой задачи еще не найдено. Трудность решения усугубляется тем, что положение этих точек на шкале определяется не только схемой и конструкцией прибора, но и технологией изготовления его элементов и узлов. На практике в качестве точек регулировки принимают начальное и конечное, среднее и конечное или начальное, среднее и конечное значения измеряемой величины в диапазоне измерения. При этом значения систематической погрешности близки к минимально возможным, поскольку в действительности точки регулировки часто располагаются близко к началу, середине или концу шкалы. Таким образом, под регулировкой средств измерения понимается совокупность операций, имеющих целью уменьшить основную погрешность до значений, соответствующих пределам ее допускаемых значений путем компенсации систематической составляющей погрешности средств измерений, т.е. погрешности схемы, мультипликативной и аддитивной погрешностей. Градуировкой называется процесс нанесения отметок на шкалы средств измерений, а также определение значений измеряемой величины, соответствующих уже нанесенным отметкам для составления градуировочных кривых или таблиц. Различают следующие способы градуировки. 1. Использование типовых шкал. Для подавляющего большинства рабочих и многих образцовых приборов используют типовые шкалы, которые изготовляются заранее в соответствии с уравнением статической характеристики идеального прибора. Если статическая характеристика линейна, то шкала оказывается равномерной. При регулировке параметрам элементов прибора экспериментально придают такие значения, при которых погрешность в точках регулировки становится равной нулю. 2. Индивидуальная градуировка шкал. Индивидуальную градуировку шкал осуществляют в тех случаях, когда статическая характеристика прибора нелинейна или близка к линейной, но характер изменения систематической погрешности в диапазоне измерения случайным образом меняется от прибора к прибору данного типа (например, вследствие разброса нелинейности характеристик чувствительного элемента) так, что регулировка не позволяет уменьшить основную погрешность до пределов ее допускаемых значений. Индивидуальную градуировку проводят в следующем порядке. На предварительно отрегулированном приборе устанавливают циферблат с еще не нанесенными отметками. К измерительному прибору подводят последовательно измеряемые величины нескольких, наперед заданных или выбранных значений. На циферблате наносят отметки, соответствующие положениям указателя при этих значениях измеряемой величины, а расстояния между отметками делят на равные части. При индивидуальной градуировке систематическая погрешность уменьшается во всем диапазоне измерения, а в точках, полученных при градуировке она достигает значения, равного погрешности обратного хода. 3. Градуировка условной шкалы. Условной называется шкала, снабженная некоторыми условными равномерно нанесенными делениями, например, через миллиметр или угловой градус. Градуировка шкалы состоит в определении при помощи образцовых мер или измерительных приборов значений измеряемой величины. В результате определяют зависимость числа делений шкалы, пройденных указателем от значений измеряемой величины. Эту зависимость представляют в виде таблицы или графика. Если необходимо избавиться и от погрешности обратного хода, градуировку осуществляют раздельно при прямом и обратном ходе. 7.5. Калибровка средств измерений По мере продвижения вверх по поверочной схеме от рабочих мер и измерительных приборов к эталонам неизбежно сокращается число мер, различных по номинальному значению. Поэтому на некоторой ступени поверочной схемы иногда разность номинальных значений поверяемой и ближайшей к ней по разряду исходной меры превышает диапазон измерения измерительного прибора соответствующей данному разряду точности. B этих случаях поверка осуществляется способом калибровки. Калибровка — способ поверки измерительных средств, заключающийся в сравнении различных мер, их сочетаний или отметок шкал в различных комбинациях и вычислении по результатам сравнений значений отдельных мер или отметок шкалы исходя из известного значения одной из них. В результате сравнения получают систему уравнений, решив которую находят действительные значения мер. Если число уравнений равно числу поверяемых мер, то действительные значения мер и погрешности их аттестации находят с помощью методов обработки результатов косвенных измерений. Однако для повышения точности аттестации мер стремятся увеличить число уравнений, и тогда действительные значения мер определяют по схеме обработки результатов совокупных измерений. Для иллюстрации способа калибровки рассмотрим следующий пример. Пример. Граммовые наборы ГН1 и ГН2, состоящие из гирь массой 500, 200, 200*, 100, 50, 20, 20*, 10, 5, 2, 2*, 1 г (звездочкой отмечены вторые гири набора того же номинала), сличают с рабочим эталоном массой в 1 кг по следующей схеме: а) рабочий эталон 1 кг = 1000 г сличают одним из методов точного взвешивания на весах 1-го разряда повышенной точности с гирями массой 500, 200, 200*, 100 г: 1000 – (500+200+200*+100) = a1, где a1 — разность между массой рабочего эталона и массой суммы гирь; б) гири 500 г набора сличают с суммой гирь массой 200, 200* и 100 г, в результате чего получают уравнение 500 – (200 +200* +100) = a2, где a2 — результат второго сличения; в) аналогично проводят остальные сличения и получают уравнения: 200 – (100 + 50 + 20 + 20* + 10) = a4, 100 – (50 + 20+ 20* + 10) = a5, 50 – (20+20*+10) = a6, 20 – (10+5+2+2*+1) = a7, 20 – (10+5+2+2*+1) = a8, 10 – (5+2+2*+1) = a9, 5 – (2+2*+1) = a10, 2 – ( 1+1*)* = a11, 2 – ( 1+1*) = a12, 1 – 1* = a13. В результате тринадцати проведенных сличений получили систему из тринадцати уравнений с тринадцатью неизвестными. Решив эту систему, найдем действительные значения масс гирь набора. Погрешности определения действительных значений могут быть вычислены способами обработки результатов косвенных измерений. 7.6. Общие методы измерений Для точных измерений величин в метрологии разработаны приемы использования принципов и средств измерений, применение которых позволяет исключить из результатов измерений ряд систематических погрешностей и тем самым освобождает экспериментатора от необходимости определять многочисленные поправки для их компенсации, а в некоторых случаях вообще является предпосылкой получения сколько-нибудь достоверных результатов. Многие из этих приемов используют при измерении только определенных величин, однако существуют и некоторые общие приемы, названные методами измерения. Наиболее просто реализуется метод непосредственной оценки, заключающийся в определении величины непосредственно по отсчетному устройству измерительного прибора прямого действия, например взвешивание на циферблатных весах, определение размера детали с помощью микрометра или измерение давления пружинным манометром. Измерения с помощью этого метода проводятся очень быстро, просто и не требуют высокой квалификации оператора, поскольку не нужно создавать специальные измерительные установки и выполнять какие-либо сложные вычисления. Однако точность измерений чаще всего оказывается невысокой из-за погрешностей, связанных с необходимостью градуировки шкал приборов и воздействием влияющих величин (непостоянство температуры, нестабильность источников питания и пр.). При проведении наиболее точных измерений предпочтение отдается различным модификациям метода сравнения с мерой, при котором измеряемую величину находят сравнением с величиной, воспроизводимой мерой. Результат измерения либо вычисляют как сумму значения используемой для сравнения меры и показания измерительного прибора, либо принимают равным значению меры. Метод сравнения с мерой, заключающийся в том, что измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на измерительный прибор сравнения, с помощью которого устанавливается соотношение между ними, называется методом противопоставления. Примером этого метода является взвешивание груза на равноплечих весах, когда измеряемая масса определяется как сумма массы гирь, ее уравновешивающих. Применение метода противопоставления позволяет значительно уменьшить воздействие на результаты измерений влияющих величин, поскольку они более или менее одинаково искажают сигналы измерительной информации как в цепи преобразования измеряемой величины, так и в цепи преобразования величины, воспроизводимой мерой. Отсчетное устройство прибора сравнения реагирует на разность сигналов, вследствие чего эти искажения в некоторой степени компенсируют друг друга. Разновидностью метода сравнения с мерой является также нулевой метод измерения, который состоит в том, что подбором размера воспроизводимой мерой величины или путем ее принудительного изменения эффект воздействия сравниваемых величин на прибор сравнения доводят до нуля. В этом случае компенсация воздействий влияющих величин оказывается более полной, а значение измеряемой величины принимается равным значению меры. При дифференциальном методе измерения на измерительный прибор (не обязательно прибор сравнения) подается непосредственно разность измеряемой величины и величины, воспроизводимой мерой. Этот метод может быть использован, конечно, только в тех случаях, когда просто и точно реализуется операция вычитания величин (длины, перемещения, электрические напряжения). Дифференциальный метод неприменим при измерении таких величин, как температура или твердость тел. К разновидностям метода сравнения с мерой относится и метод замещения, широко применяемый в практике точных метрологических исследований. Сущность метода в том, что измеряемая величина замещается в измерительной установке некоторой известной величиной, воспроизводимой мерой. Замещение может быть полным или неполным, в зависимости от чего говорят о методе полного или неполного замещения. При полном замещении показания не изменяются и результат измерения принимается равным значению меры. При неполном замещении для получения значения измеряемой величины к значению меры следует прибавить величину, на которую изменилось показание прибора. Преимущество метода замещения - в последовательном во времени сравнении измеряемой величины и величины, воспроизводимой мерой. Благодаря тому, что обе эти величины включаются одна за другой в одну и ту же часть измерительной цепи прибора, точностные возможности измерений значительно повышаются по сравнению с измерениями, проводящимися с помощью других разновидностей метода сравнения, где несимметрия цепей, в которые включаются сравниваемые величины, приводит к возникновению систематических погрешностей. Способ замещения применяется при электрических измерениях с помощью мостов переменного тока, условие равновесия которых определяется не только значениями величин, воспроизводимых элементами плеч моста, но также и влиянием паразитных токов, емкостей, индуктивностей и рядом других факторов. Эти причины вызывают появление погрешностей, которые могут быть исключены, если проводить измерения методом замещения. Для этого вначале мост уравновешивается с включенной в его цепь измеряемой величиной, которая затем замещается известной величиной, и мост уравновешивается вновь. Если при этом никаких изменений ни в мосте, ни во внешних условиях не происходит, то указанные выше погрешности исключаются почти полностью. Одним из общих методов измерений является метод совпадений, представляющий собой разновидность метода сравнения с мерой. При проведении измерений методом совпадений разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов. По принципу метода совпадений построен нониус, входящий в состав ряда измерительных приборов. Так, например, шкала нониуса штангенциркуля имеет десять делений через 0.9 мм. Когда нулевая отметка шкалы нониуса оказывается между отметками основной шкалы штангенциркуля, это означает, что к целому числу миллиметров необходимо добавить число десятых долей миллиметра, равное порядковому номеру совпадающей отметки нониуса. В рамках перечисленных выше методов измерений в метрологической практике и в общем приборостроении часто применяются специальные приемы для исключения самих источников систематических погрешностей или их компенсации. Рассмотрим наиболее употребительные из этих приемов. Параметрическая стабилизация очень широко применяется при ответственных измерениях. Этот прием используют для поддержания в заданных пределах температуры и влажности окружающей среды, напряжения питания и других. Наиболее распространены такие способы параметрической стабилизации, как термостатирование приборов, защита от воздействия вибраций, использование эффективных стабилизаторов в цепях электропитания приборов, экранирование приборов для защиты их от воздействия посторонних электрических, магнитных, радиационных и других полей. Применение этих способов иногда позволяет избежать введения в результаты измерения поправок. Параметрическая стабилизация очень широко применяется при ответственных измерениях. Этот прием используют для поддержания в заданных пределах температуры и влажности окружающей среды, напряжения питания и других. Наиболее распространены такие способы параметрической стабилизации, как термостатирование приборов, защита от воздействия вибраций, использование эффективных стабилизаторов в цепях электропитания приборов, экранирование приборов для защиты их от воздействия посторонних электрических, магнитных, радиационных и других полей. Применение этих способов иногда позволяет избежать введения в результаты измерения поправок. Способ компенсации постоянных и периодических погрешностей по знаку. При реализации этого способа процесс измерения строится таким образом, что постоянная систематическая погрешность входит в результат измерения один раз с одним знаком, а другой раз — с другим. Тогда среднее из двух полученных результатов оказывается свободным от постоянной погрешности. Способ вспомогательных измерений применяется в тех случаях, когда воздействие влияющих величин на результаты измерений вызывает большие погрешности измерений. Тогда идут на заведомое усложнение схемы измерительной установки, включая в нее элементы, воспринимающие значение влияющих величин, автоматически вычисляющие соответствующие поправки и вносящие их в полезные сигналы, которые поступают на отсчетные или регулирующие устройства. Способ вспомогательных измерений в большой степени относится к инструментальным методам борьбы с систематическими погрешностями, поэтому в рамках настоящего курса не рассматривается. Вообще следует заметить, что многие из приведенных методов и приемов исключения систематических погрешностей в настоящее время все в большей степени реализуются схемами самих измерительных средств. В результате разработка методологии измерений приобретает все большее значение непосредственно для проектирования измерительной аппаратуры. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

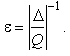
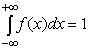 — вероятность достоверного события равна 1;
— вероятность достоверного события равна 1; 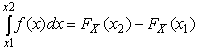 — вероятность попадания случайной величины в интервал от x1 до x2.
— вероятность попадания случайной величины в интервал от x1 до x2. 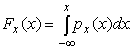 (7)
(7)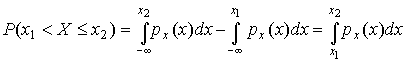 (8)
(8)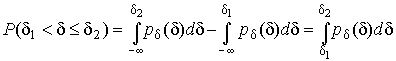 (9)
(9)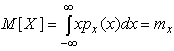 (10)
(10) (14)
(14)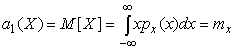 (15)
(15)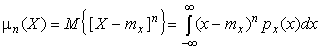 (16)
(16)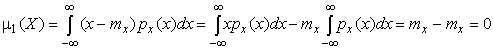 (17)
(17)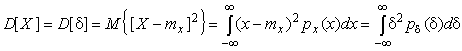 (18)
(18)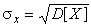 (19)
(19)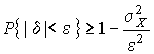 или
или 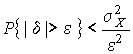 (20)
(20)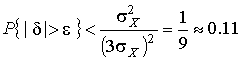
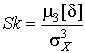 (21)
(21)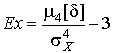 (22)
(22)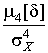 потому, что для широко распространенного нормального распределения погрешностей μ4[δ]=3σ4x. Таким образом, для нормального распределения эксцесс равен нулю, более плосковершинные распределения обладают отрицательным эксцессом, более островершинные — положительным (рис.5).
потому, что для широко распространенного нормального распределения погрешностей μ4[δ]=3σ4x. Таким образом, для нормального распределения эксцесс равен нулю, более плосковершинные распределения обладают отрицательным эксцессом, более островершинные — положительным (рис.5).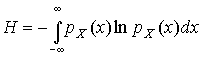
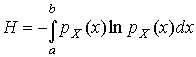 при наличии ограничивающих условий:
при наличии ограничивающих условий: 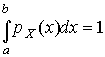 ,
, 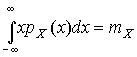 ,
, 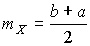 — математическое ожидание результатов наблюдений. Решение поставленной задачи находится методом множителей Лагранжа.
— математическое ожидание результатов наблюдений. Решение поставленной задачи находится методом множителей Лагранжа.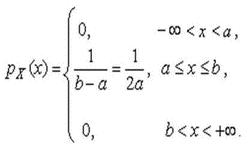 (23)
(23)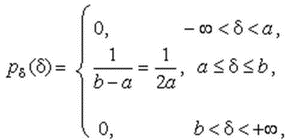 (24)
(24)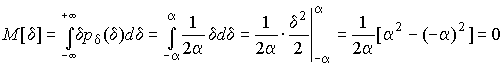
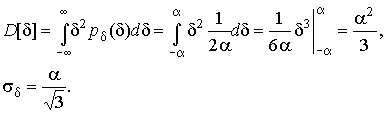
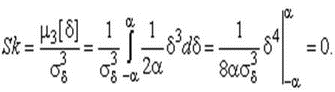
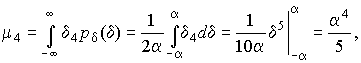
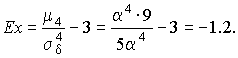
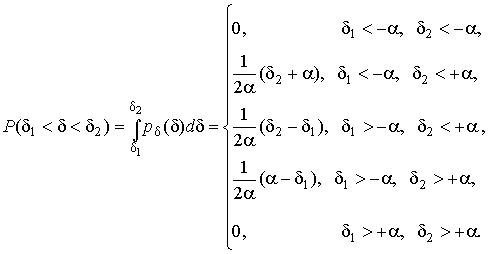
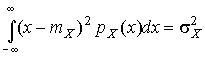 .
.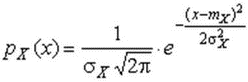 (25)
(25)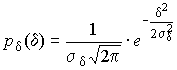 (25)
(25)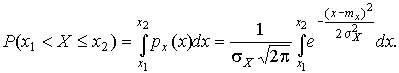
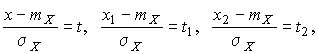
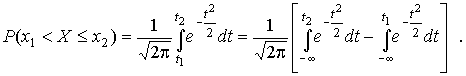
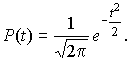 (27)
(27)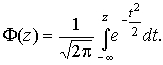 (28)
(28)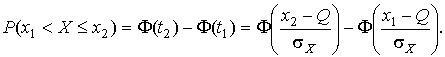 (29)
(29)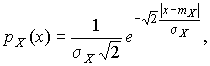 (30)
(30)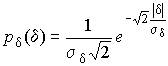
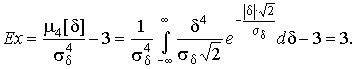
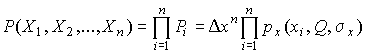
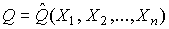 и
и 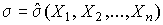 вероятность получения экспериментальных данных P(X1, X2, …, Xn) достигает наибольшего значения. В соответствии с методом максимального правдоподобия именно эти значения и принимаются в качестве точечных оценок истинного значения и среднеквадратического отклонения результатов наблюдений.
вероятность получения экспериментальных данных P(X1, X2, …, Xn) достигает наибольшего значения. В соответствии с методом максимального правдоподобия именно эти значения и принимаются в качестве точечных оценок истинного значения и среднеквадратического отклонения результатов наблюдений.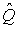 и
и 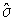 , при которых функция правдоподобия
, при которых функция правдоподобия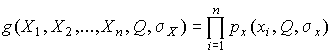 (31)
(31)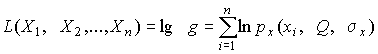 (32)
(32)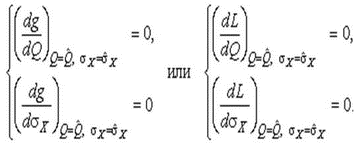 (33)
(33)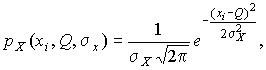
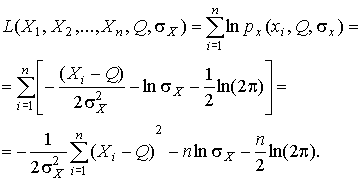
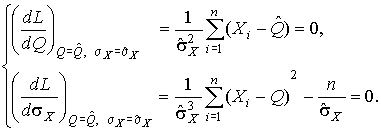
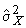 :
: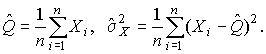
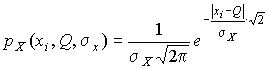
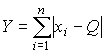 принимает наименьшее значение. Поэтому задача об отыскании оценки истинного значения сводится к определению такого значения
принимает наименьшее значение. Поэтому задача об отыскании оценки истинного значения сводится к определению такого значения 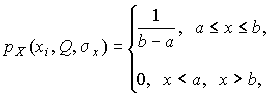
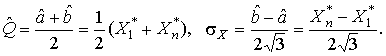
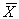 из результатов отдельных наблюдений Xi,
из результатов отдельных наблюдений Xi,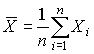 .
.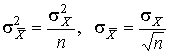 .
.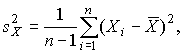
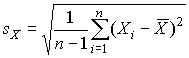
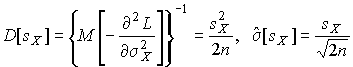 .
.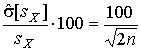
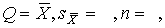
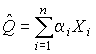 , где αi — некоторые постоянные, именно среднее арифметическое
, где αi — некоторые постоянные, именно среднее арифметическое 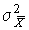 . Поэтому для случая нормально распределенных случайных погрешностей оценки, получаемые методом наименьших квадратов, совпадают с оценками максимального правдоподобия.
. Поэтому для случая нормально распределенных случайных погрешностей оценки, получаемые методом наименьших квадратов, совпадают с оценками максимального правдоподобия.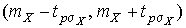 . Согласно формуле (29)
. Согласно формуле (29)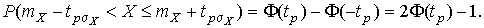
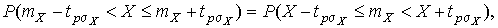
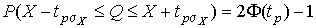 (34)
(34)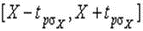 .
. 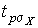 называется доверительной границей случайного отклонения результатов наблюдений, соответствующей доверительной вероятности Р. Для определения доверительной границы (при выполнении перечисленных условий) задаются доверительной вероятностью, например Р=0.95 или Р=0.995 и по формулам
называется доверительной границей случайного отклонения результатов наблюдений, соответствующей доверительной вероятности Р. Для определения доверительной границы (при выполнении перечисленных условий) задаются доверительной вероятностью, например Р=0.95 или Р=0.995 и по формулам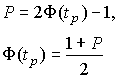 (35)
(35)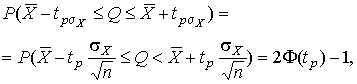 (36)
(36)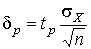 (37)
(37)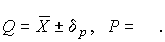 (38)
(38)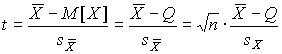 (39)
(39)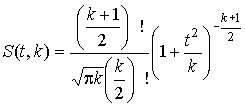 (40)
(40)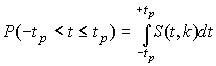
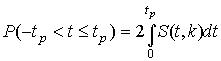
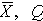 и
и 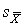 , получим окончательно
, получим окончательно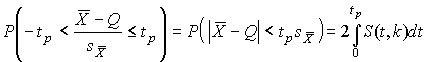 (41)
(41)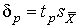 , например
, например 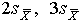 и т.д. Итог измерений записывается в виде
и т.д. Итог измерений записывается в виде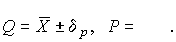 (42)
(42)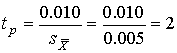
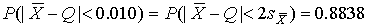 .
.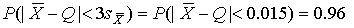
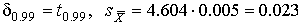 мм.
мм.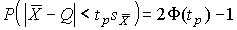
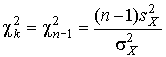 (43)
(43)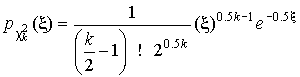 (44)
(44)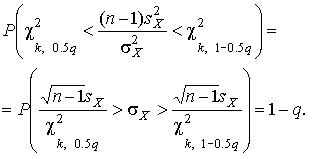 (46)
(46)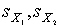 ], границы которого равны
], границы которого равны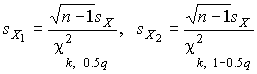 (47)
(47)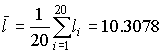 мм.
мм.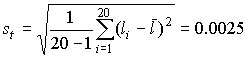 мм.
мм.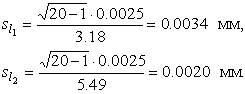
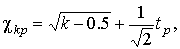
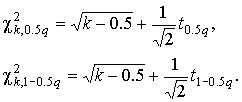 (49)
(49)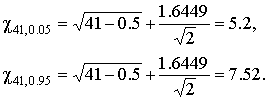
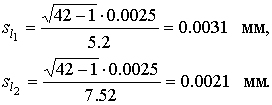
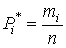 (50)
(50)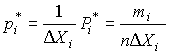 (51)
(51)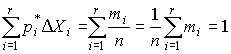
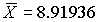 мм, sX=0.0028 мм и уравнение кривой нормального распределения, лучше всего согласующегося со статистическим распределением, должно иметь вид:
мм, sX=0.0028 мм и уравнение кривой нормального распределения, лучше всего согласующегося со статистическим распределением, должно иметь вид: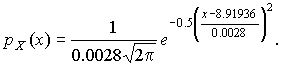
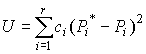 (52)
(52)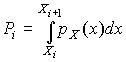 , (53)
, (53)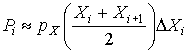 . (54)
. (54)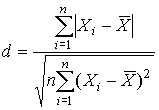 . (55)
. (55)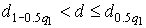 ,
, 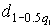 и
и 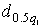 — квантили, выбираемые из табл. П.8.
— квантили, выбираемые из табл. П.8. 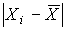 превосходят уровень sXZ0.5(1+α), где sX — оценка среднеквадратического отклонения результатов наблюдения, Z0.5(1+α) — квантиль интегральной функции нормированного нормального распределения, определяемый по данным табл. П.2 приложения при значении
превосходят уровень sXZ0.5(1+α), где sX — оценка среднеквадратического отклонения результатов наблюдения, Z0.5(1+α) — квантиль интегральной функции нормированного нормального распределения, определяемый по данным табл. П.2 приложения при значении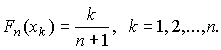 (56)
(56)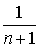 , если все n членов ряда различны. Если же для некоторого k X*(k)=X*(k+1)≤…≤X*(k+i), то Fn(x) в точке x=Xk возрастает на
, если все n членов ряда различны. Если же для некоторого k X*(k)=X*(k+1)≤…≤X*(k+i), то Fn(x) в точке x=Xk возрастает на 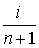 , где i – число равных между собой членов ряда.
, где i – число равных между собой членов ряда.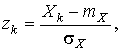
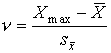 или
или 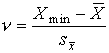 . (57)
. (57)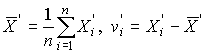 . (58)
. (58)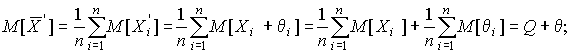
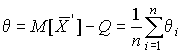 .
.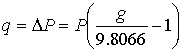 ,
, 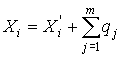 , (60)
, (60)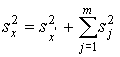 , (61)
, (61) 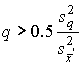 . (62)
. (62) 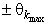 или имеют определенные средние квадратические отклонения
или имеют определенные средние квадратические отклонения 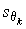 . В первом случае для неисключенных остатков следует принять равномерное распределение, во втором — нормальное. Дисперсия суммы неисключенных остатков систематической погрешности определяется как сумма их дисперсий и поэтому
. В первом случае для неисключенных остатков следует принять равномерное распределение, во втором — нормальное. Дисперсия суммы неисключенных остатков систематической погрешности определяется как сумма их дисперсий и поэтому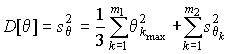 , (63)
, (63) 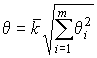 , (64)
, (64) 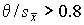 , то систематической погрешностью можно пренебречь и определить доверительные границы погрешности результата как доверительные границы случайной погрешности
, то систематической погрешностью можно пренебречь и определить доверительные границы погрешности результата как доверительные границы случайной погрешности 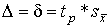 при P=0.95 (и при P=0.99); если же выполняется условие
при P=0.95 (и при P=0.99); если же выполняется условие 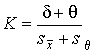 (65)
(65)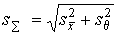 находят квадратическим суммированием дисперсии случайной
находят квадратическим суммированием дисперсии случайной 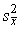 и систематической s²θ погрешности результата, определяемой формулой (63). Границы случайной δ и систематической θ погрешности, входящие в формулу (65), необходимо выбирать при одной и той же доверительной вероятности (P=0.95 или P=0.99).
и систематической s²θ погрешности результата, определяемой формулой (63). Границы случайной δ и систематической θ погрешности, входящие в формулу (65), необходимо выбирать при одной и той же доверительной вероятности (P=0.95 или P=0.99). 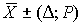 , а при отсутствии сведений о виде функции распределения составляющих погрешности и необходимости дальнейшей обработки результатов и анализа погрешностей — в виде
, а при отсутствии сведений о виде функции распределения составляющих погрешности и необходимости дальнейшей обработки результатов и анализа погрешностей — в виде 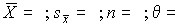 .
.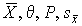 .
.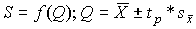 и f — непрерывная дифференцируемая функция в окрестности точки
и f — непрерывная дифференцируемая функция в окрестности точки 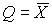 .
.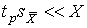 . Тогда
. Тогда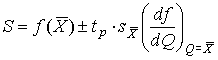 . (66)
. (66)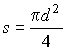 .
.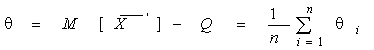 .
.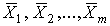 — средние арифметические m рядов равнорассеянных результатов наблюдений постоянной физической величины Q;
— средние арифметические m рядов равнорассеянных результатов наблюдений постоянной физической величины Q; 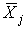 (j=1, 2,…, m) с дисперсиями
(j=1, 2,…, m) с дисперсиями 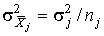 :
: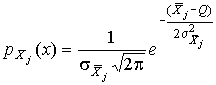 ,
,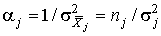 .
.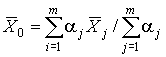 . (67)
. (67)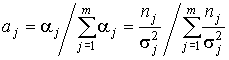 , (68)
, (68)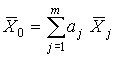 . (69)
. (69)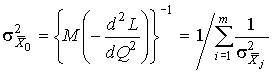 . (70)
. (70)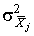 неизвестны, то пользуются их оценками
неизвестны, то пользуются их оценками 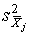 , с помощью которых определяют веса или весовые коэффициенты.
, с помощью которых определяют веса или весовые коэффициенты.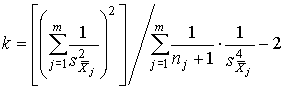 . (71)
. (71)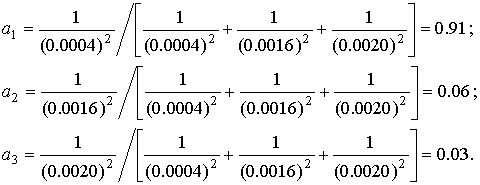
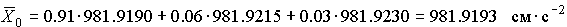
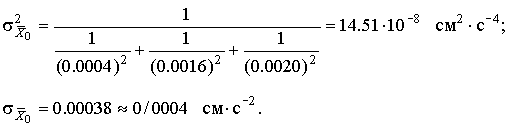
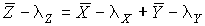 , (73)
, (73)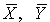 — средние арифметические (или средние взвешенные), полученные при обработке результатов прямых измерений величин QX и QY, λX и λY — случайные погрешности средних,
— средние арифметические (или средние взвешенные), полученные при обработке результатов прямых измерений величин QX и QY, λX и λY — случайные погрешности средних, 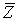 и λZ — оценка истинного значения косвенно измеряемой величины и его случайная погрешность.
и λZ — оценка истинного значения косвенно измеряемой величины и его случайная погрешность. 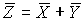 , λZ = λX – λY, (74)
, λZ = λX – λY, (74)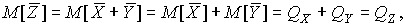
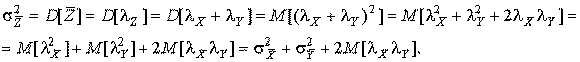
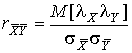 . (75)
. (75)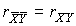 .
.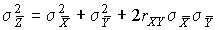 . (76)
. (76)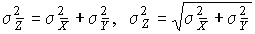 . (77)
. (77)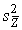 дисперсии результата косвенных измерений через оценки дисперсий
дисперсии результата косвенных измерений через оценки дисперсий 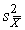 и
и 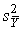 :
: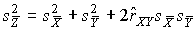 . (78)
. (78)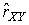 вычисляют на основании результатов прямых измерений исходных величин:
вычисляют на основании результатов прямых измерений исходных величин: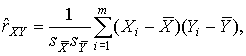 (79)
(79)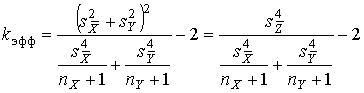 , (80)
, (80)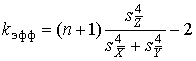 . (81)
. (81)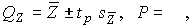
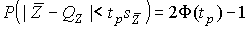
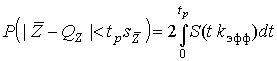 .
.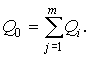 (82)
(82)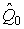 истинного значения измеряемой величины Q0 принимается сумма оценок
истинного значения измеряемой величины Q0 принимается сумма оценок 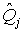 истинных значений слагаемых:
истинных значений слагаемых: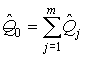 . (83)
. (83)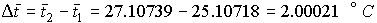 ,
,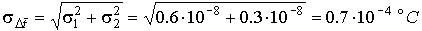 .
.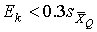 ,
,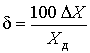 . (86)
. (86)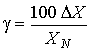 . (87)
. (87)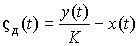 . (88)
. (88)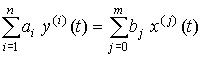 , (89)
, (89)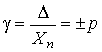 , (92)
, (92)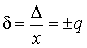 , (93)
, (93)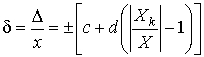 , (94)
, (94)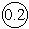 .
.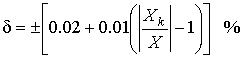 .
.