Глава 29. ЕЩЕ ДЕВЯТЬ ЗАДАЧ

1. Как пересечь пустыню? На одном краю пустыни шириной 800 миль имеется неограниченный запас бензина. В самой пустыне заправочных станций нет и бензина достать негде. Грузовик может перевозить столько бензина, сколько необходимо для того, чтобы проехать 500 миль (это количество мы будем называть одной заправкой). Кроме того, его экипажу разрешается строить заправочные станции в любом месте трассы. Бензохранилища могут быть любых размеров; предполагается, что потерь на испарение нет.

Какое количество бензина (в заправках) необходимо для того, чтобы грузовик мог пересечь пустыню? Существует ли предельная ширина пустыни, которую можно пересечь на грузовике?

2. Двое детей. У мистера Смита двое детей. По крайней мере один из них мальчик. Какова вероятность того, что оба ребенка мистера Смита — мальчики?

У мистера Джонсона двое детей. Старший ребенок девочка. Какова вероятность того, что оба ребенка мистера Джонсона — девочки?

3. Шахматная задача лорда Дансэни. Поклонникам ирландского писателя лорда Дансэни вряд ли нужно говорить о том, что лорд Дансэни любил шахматы (его рассказ «Гамбит трех моряков», несомненно, самая занимательная из когда-либо написанных шахматных новелл). Однако не столь широко известно, что он любил придумывать хитроумные шахматные задачи, в которых так же, как и в его рассказах, сочетались юмор и фантазия.

На рис. 152 изображена задача, которую Дансэни предложил для сборника «В часы досуга». Для ее решения умение логически мыслить требуется в гораздо большей степени, чем умение играть в шахматы (хотя правила игры знать необходимо). Белые начинают и дают мат в четыре хода. Изображенная на рис. 152 позиция может встретиться и в реальной партии.

Рис. 152 Шахматная задача лорда Дансэни.

4. Профессор на эскалаторе. Польский математик профессор Станислав Шляпенарский, идя очень медленно по движущемуся вниз эскалатору, успевает спуститься на 50 ступеней, прежде чем эскалатор кончается. Из любопытства он взбегает затем по тому же эскалатору (не пропуская при этом ни одной ступени) и оказывается наверху после того, как преодолеет 125 ступеней.

Сколько ступеней можно будет насчитать в остановившемся эскалаторе, если предположить, что вверх профессор взбегает в пять раз быстрее, чем спускается вниз (то есть за то время, за которое, идя вниз, профессор опускается на одну ступеньку, взбегая наверх, он успевает подняться на пять ступенек)?

5. Одинокая восьмерка. Редакторы журнала The American Mathematical Monthly обнаружили, что самой популярной из когда-либо напечатанных журналом задач является задача, присланная Р. Л. Шэссэном (April 1964).

Наш добрый знакомый и известный знаток теории чисел профессор Евклид Парацельсо Бомбасто Умбигио страшно занят проверкой на своем арифмометре 81 х 10⁹ возможных решений следующей задачи. Требуется восстановить запись деления столбиком одного числа на другое (деление производится без остатка), в которой все цифры подряд были заменены на X, за исключением цифр в частном, где они почти все оказались стертыми:

Посрамите профессора! Докажите, что число возможных решений можно понизить до (81 х 10⁹)⁰.

Поскольку любое отличное от нуля число в нулевой степени равно единице, читатель должен найти единственно возможное решение задачи. Цифра 8 в частном стоит на правильном месте: восьмерка является третьей цифрой пятизначного ответа. Задача легче, чем может показаться на первый взгляд, и решается без особого труда, если воспользоваться некоторыми вполне элементарными соображениями.

6. Как разделить пирог? Существует простой способ, при котором двое могут разделить пирог так, чтобы каждому досталась по крайней мере половина: один разрезает пирог, а другой выбирает себе кусок. Придумайте общий метод, который позволил бы n персонам разделить пирог на п частей так, чтобы каждому досталось не меньше, чем по 1/n пирога.

7. Складывание карты. Математикам и по сей день не удалось найти формулу для числа способов, которыми можно сложить дорожную карту при заданном числе n сгибов. Некоторое представление о сложности этого вопроса дает следующая головоломка, придуманная все тем же Генри Э. Дьюдени.

Разделите прямоугольный листок бумаги на восемь квадратов и перенумеруйте их (только с одной стороны листа) так, как показано на рис. 153 вверху.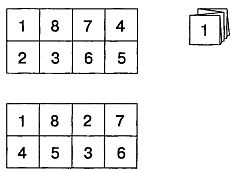

Рис. 153 Головоломка Дьюдени со складыванием карты.

Существует 40 различных способов перегибания этой «карты» вдоль проведенных прямых, при которых на верхнем квадрате после складывания оказывается цифра 1. Карту требуется складывать так, чтобы цифры на квадратах шли последовательно от 1 до 8, причем квадрат с цифрой 1 был наверху.

Если вам удалось решить эту задачу, постарайтесь решить более сложную: попробуйте сложить таким же образом «карту», изображенную на рис. 153 внизу.

8. Рассеянный кассир. Рассеянный кассир, оплачивая чек мистеру Брауну, перепутал доллары и центы и отсчитал клиенту доллары вместо центов и центы вместо долларов. Купив газету за пять центов, Браун обнаружил, что денег у него ровно вдвое больше, чем он должен получить по чеку. На какую сумму был выписан чек?

9. Вода и вино. В уже упоминавшейся задаче с таким названием говорилось о двух сосудах, в одном из которых содержалось вино, а в другом вода. Некоторое количество воды наливают в вино, а затем то же количество смеси переливают снова в сосуд с водой.

Спрашивается, чего больше: воды в вине или вина в воде? Ответ: количество воды в сосуде с вином и вина в сосуде с водой одинаково.

Раймонд Смаллиан поставил новый вопрос. Предположим, что сначала в одном сосуде находится 10 унций воды, а в другом 10 унций вина. Если из первого сосуда во второй и обратно переливать любое число раз по три унции жидкости (тщательно перемешивая содержимое сосуда после каждого переливания), то может ли наступить момент, когда процентное содержание вина в сосудах станет одинаковым?

Ответы

1. Приводимое ниже решение задачи о том, как пересечь пустыню, заимствовано из журнала Eureka, издаваемого студентами-математиками университета в Кеймбридже (Массачусетс). Назовем «единицей» расстояние в 500 миль, одной заправкой — количество бензина, необходимое для того, чтобы проехать 500 миль, и рейсом — поездку, совершаемую грузовиком в любом направлении от одной остановки до другой.

Две заправки позволяют грузовику пройти максимальное расстояние в 4/3 единицы. Для этого необходимо совершить четыре рейса. Сначала на расстоянии 1/3 единицы от пункта отправления строится бензохранилище: грузовик полностью заправляют (на это уходит 1 заправка), после чего он едет к бензохранилищу, оставляет там 1/3 заправки и возвращается назад. Его снова полностью заправляют (на что уходит еще 1 заправка). Он опять едет к бензохранилищу и забирает оставленную там 1/3 заправки (таким образом, он снова оказывается полностью заправленным). После этого он может проехать еще расстояние в 1 единицу.

Три заправки позволят грузовику проехать расстояние в 4/3 + 1/5 единицы, причем для этого потребуется совершить девять рейсов.

Сначала на расстоянии 1/5 единицы от пункта отправления строят бензохранилище и завозят в него 6/5 заправки. На это уходят три рейса. Затем грузовик возвращается, полностью заправляется (на что уходит последняя заправка) и прибывает к первому хранилищу, имея в своих баках 4/5 заправки. Вместе с уже имеющимся в бензохранилище топливом это количество составляет две полные заправки, что достаточно для того, чтобы грузовик мог пройти еще 4/3 единицы расстояния (как это сделать, мы только что объяснили).

Нам осталось еще ответить на второй вопрос о минимальном количестве бензина, необходимом для того, чтобы грузовик мог проехать 800 миль. Три заправки, как мы только что выяснили, позволяют грузовику покрыть расстояние в 766∙2/3 мили (4/3 +1/5 единицы), поэтому на расстоянии 33∙1/3 мили (1/15 единицы) от пункта отправления необходимо построить еще одно (третье) бензохранилище. За пять рейсов экипаж грузовика сможет построить это хранилище и завезти в него столько горючего, что, когда в конце седьмого рейса грузовик поравняется с третьим хранилищем, общее количество бензина в его баках и в хранилище составит три заправки.

Как мы уже знаем, этого количества топлива достаточно для того, чтобы грузовик смог пройти оставшееся расстояние в 766∙2/3 мили. На семь рейсов, совершенных между пунктом отправления и вновь построенным бензохранилищем, израсходовано 7/15 заправки.

Трех оставшихся заправок как раз достаточно для того, чтобы проехать оставшуюся часть пути. Таким образом, на весь путь будет израсходовано 3∙7/15, или больше 3,46, заправки. Всего потребуется совершить шестнадцать рейсов.

Рассуждая в том же духе, можно показать, что, имея четыре заправки, грузовик сумеет проехать расстояние в 1∙1/3 +1/5 + 1/7 единицы.

На границах отрезков пути длиной в 1∙1/3, 1/5 и 1/7 следует расположить бензохранилища. С увеличение числа заправок этот бесконечный ряд расходится, поэтому грузовик сможет пересечь пустыню любой ширины. Если ширина пустыни 1000 миль, то для преодоления этого расстояния потребуется построить 7 бензохранилищ, совершить 64 рейса и израсходовать 7,673 заправки бензина.

В связи с этой задачей редакция получила сотни писем с общими решениями и интересными замечаниями. Сесил Дж. Филлинс, профессор математики Флоридского университета, следующим образом сформулировала существо дела.

Общее решение задачи дается формулой

где d— ширина пустыни, которую необходимо пересечь, m — число миль, отнесенных к одной заправке бензина. Число бензохранилищ, которое необходимо построить, на единицу меньше числа членов в отрезке ряда, который следует взять для получения данного d. На поездки между любыми двумя станциями расходуется одна заправка. Поскольку ряд расходится, метод позволяет преодолеть пустыню любой ширины, хотя необходимое количество бензина с увеличением расстояния возрастает экспоненциально.

Если грузовик в конце путешествия возвращается в исходный пункт, то формула имеет вид

Этот ряд также расходится, и свойства решения аналогичны свойствам решения для случая, когда грузовик обратно не возвращается.

2. Если у Смита двое детей и по крайней мере один из них мальчик, то мы имеем три равновероятных случая:

мальчик — мальчик,

мальчик — девочка,

девочка — мальчик.

Только в одном из них оба ребенка — мальчики, следовательно, вероятность того, что у Смита два сына, равна 1/3.

В случае Джонса ситуация иная. Из условия задачи нам известно, что старший ребенок девочка. Это ограничивает число возможных случаев лишь двумя равновероятными исходами:

девочка — девочка,

девочка — мальчик.

Следовательно, вероятность того, что у Джонса две девочки, равна 1/2.

Однако, поразмыслив, я понял, что задача сформулирована неоднозначно и дать на нее правильный ответ без использования дополнительных данных невозможно. Дальнейший анализ задачи дан в главе 34.

3. Ключом к шахматной задаче лорда Дансэни служит то обстоятельство, что черный ферзь стоит не на черном поле, как он должен был бы стоять в начале игры. Значит, черный король и черный ферзь уже успели совершить какие-то ходы, что возможно лишь в том случае, если некоторые из черных пешек также совершили какие-то ходы. Пешки не могут ходить назад, отсюда мы с необходимостью заключаем, что черные пешки занялиизображенную на рис. 152 позицию, двигаясь от противоположного края доски! Зная это, нетрудно заметить, что белым конем, стоящим на g1, можно поставить мат в четыре хода. Первым ходом конь белых перепрыгивает с поля g1 на поле g2. Если черные отвечают ходом КЬ8—а6, то белые дают мат уже через два хода, однако черные могут отсрочить свое поражение на один ход, пойдя КЬ8—с6 вместо КЬ8—а6. Очередным ходом Ке2—f4 белые угрожают объявить мат на следующем ходу. Чтобы закрыться от мата, черные делают ход Кс6—d4. Белые берут коня черным ферзем, после чего дают мат на четвертом ходу.

4. Пусть n — число ступеней на видимой части стоящего эскалатора. Время, за которое профессор Шляпенарский успевает спуститься на одну ступеньку, примем за единицу. Поскольку для того, чтобы спуститься по движущемуся вниз эскалатору, профессору необходимо пройти 50 ступеней, за время спуска (равное 50 единицам) под гребенкой эскалатора исчезают и становятся невидимыми n—50 ступеней. Поднимаясь наверх (против движения) по тому же эскалатору, профессор преодолевает 125 ступеней, проходя за каждую единицу времени 5 ступеней. Следовательно, в принятых нами единицах время подъема составляет — 125/5, или 25 единиц, и под гребенкой эскалатора успевают исчезнуть 125 — n ступеней. Поскольку эскалатор можно считать движущимся с постоянной скоростью, для n получается следующее линейное уравнение:

из которого уже нетрудно найти ответ задачи: n = 100.

5. Когда при делении столбиком приходится сносить не одну, а две цифры, в частном появляется нуль. В нашем примере это происходит дважды, поэтому мы сразу же сможем сказать, что частное имеет вид Х080Х. При умножении делителя на последнюю цифру частного должно получиться четырехзначное число. Поэтому последней цифрой частного может быть только 9, так как умноженный на 8 делитель дает лишь трехзначное число.

Делитель не может быть больше или равным 125, так как, умножив 125 на 8, мы получим 1000, то есть четырехзначное число. Отсюда следует вывод, что первая цифра частного должна быть больше 7, так как, умножив на 7 делитель (по доказанному он меньше 125), мы бы получили число, которое после вычитания из первых четырех знаков делимого давало бы не двузначный, а по крайней мере трехзначный остаток. Так как девятка не может быть первой цифрой частного (при умножении делителя на 9 мы получили бы четырехзначное число), то ею может быть лишь восьмерка. Итак, частное полностью известно и равно 80809.

Делитель должен быть больше 123, так как произведение 80 809 на 123 выражается семизначным числом, а наше делимое восьмизначно. Единственное натуральное число, заключенное между 123 и 125, равно 124. Теперь уже мы в состоянии восстановить всю запись деления:

6. Разделить пирог между n персонами так, чтобы каждой из них досталось по крайней мере 1/n пирога, можно несколькими способами. Предлагаемый нами способ обладает тем преимуществом, что после раздела не остается лишних кусков пирога.

Предположим, что имеется пять желающих получить по куску пирога: А, В, С, D и Е. А отрезает кусок, который, по его мнению, составляет 1/5 пирога, и намеревается оставить его себе. Если В считает, что А отрезал слишком большой кусок, то он (В) имеет право уменьшить этот кусок до размеров, которые он считает соответствующими 1/5 пирога. Разумеется, если В считает, что отрезанный А кусок меньше 1/5, то он к нему вообще не прикасается. Аналогичными правами пользуются по очереди С, D и Е. Кусок достается тому из пятерых, кто дотрагивается до него последним. Всякий, кто считает, что получившему кусок пирога досталось меньше 1/5, естественно, доволен: ведь, по его мнению, осталось больше 4/5 пирога.

Оставшаяся часть пирога (сюда входят и кусочки, отрезанные при доведении уже отрезанного куска до «кондиции») делится затем точно таким же образом между четырьмя, тремя и т. д. любителями пирога. При последнем разделе один из участников режет пирог, а другой выбирает. Ясно, что этот метод применим при любом числе заинтересованных лиц.

Подробный разбор этого и других решений задачи содержится в книге Р. Д. Льюиса и Г. Райффа «Игры и решения» (ИЛ, 1960).

7. Вот как нужно складывать первую карту. Перевернем ее лицевой стороной вниз, в результате чего номера на квадратах расположатся в такой последовательности:

Затем, перегнув карту пополам, сложим ее так, чтобы правая половина карты накрыла ее левую половину, то есть квадрат 5 оказался

наложенным на квадрат 2, квадрат 6 — на квадрат 3, квадрат 4 — на квадрат 1 и квадрат 7 — на квадрат 8. Сложенную вдвое карту перегнем еще раз пополам так, чтобы ее нижняя половина накрыла верхнюю половину. При этом квадрат 4 накроет квадрат 5, а квадрат 7 — квадрат 6. Внутреннюю часть карты сложим еще раз пополам так, чтобы квадраты 4 и 5 оказались между квадратами 6 и 3, а затем подогнем край карты (квадраты 1 и 2) под образовавшийся пакетик. Первая карта свернута по всем правилам!

Вторую карту сначала нужно сложить пополам (номерами квадратов наружу), перегнув ее по горизонтали так, чтобы сверху оказались квадраты с номерами 4, 5, 3 и 6. Затем следует отогнуть левый край двойной полосы так, чтобы квадрат 4 накрыл собой квадрат 5. Правый конец полоски (квадраты 6 и 7) после этого нужно ввести внутрь сложенной вдвое карты между квадратами 1 и 4 и протащить за то ребро квадрата 4, по которому уже был произведен сгиб, так чтобы квадраты 6 и 7 оказались между квадратами 8 и 5, а квадраты 3 и 2 — между квадратами 1 и 4.

8. Пусть x — число долларов, а у — число центов в той сумме, на которую мистер Браун выписал чек. Условие задачи можно записать в виде уравнения

100y + x — 5 = 2(100x + y),

или, что то же самое,

99y — 199x = 5

Это диофантово уравнение, имеющее бесконечно много решений в целых числах. Обычный метод решения с помощью непрерывных дробей дает наименьший ответ в положительных целых числах х = 31, у = 63. Следовательно, мистер Браун выписал чек на сумму 31 доллар 63 цента. Это единственный ответ задачи, поскольку ближайшее к найденному решение х = 129, у = 262 не удовлетворяет требованию: у должен быть меньше 100.[51]

Однако существует гораздо более простой подход к решению.

Пусть, как и прежде, х означает число долларов, а у — число центов. После покупки газеты у Брауна осталось денег 2х + 2у. При этом из х центов, выплаченных ему кассиром, у него осталось х-5 центов.

Мы знаем, что у меньше 100, но мы не можем сказать с уверенностью, будет ли у меньше 50 центов. Если это так, то мы вправе записать уравнения

2x = y

2y = x-5

Если у равен 50 или большему количеству центов, то после покупки газеты у Брауна останется 2у центов, что больше или равно числу оставшихся у него долларов. Поэтому в написанные нами уравнения в этом случае необходимо внести некоторые изменения:

из 2у вычесть 100 и прибавить 1 к 2х. Уравнения примут вид

2x+1 = y

2y-100 = x-5

Каждая из систем уравнений легко решается. Первая система приводит к отрицательному значению х, что исключается. Вторая дает правильный ответ.

9. Независимо от того, сколько вина в одном сосуде и сколько воды в другом, а также от того, сколько жидкости переносится из сосуда в сосуд за один раз (за исключением единственного случая, когда в одном из сосудов вообще нет жидкости), достичь равенства процентного содержания вина в обеих смесях невозможно. Это нетрудно доказать с помощью простого рассуждения по индукции.

Если в сосуде А содержится вино более высокой концентрации, чем в сосуде В, то и после того, как мы отольем часть жидкости из А в В, в А останется вино более высокой концентрации. Точно так же, переливая вино из В в А, то есть из сосуда с вином низкой концентрации в сосуд с вином более высокой концентрации, мы заведомо оставляем в В вино более низкой по сравнению с А концентрации.

Так как при каждом переливании могут представляться только эти два случая, то в сосуде А всегда будет смесь с более высоким процентным содержанием вина, чем в В. Единственный способ уравнивания концентраций заключается в том, чтобы полностью перелить содержимое одного из сосудов в другой.

Только что приведенное решение исходит из неверного допущения: оно предполагает, что жидкости бесконечно делимы, в то время как они состоят из дискретных молекул. На это указал мне в своем письме один из читателей.

Сэр!

Ваше решение задачи о смешивании вина и воды явно игнорирует физическую природу рассматриваемых объектов. Когда из смеси двух жидкостей берут пробу, то относительное количество одной из жидкостей в пробе будет отличаться от относительного количества той оке жидкости в смеси. Отклонение от «правильного» относительного количества будет порядка

, где n — число молекул интересующей нас жидкости.

Следовательно, уравнять концентрации вина в двух сосудах можно. Вероятность выравнивания концентраций становится заметно отличной от нуля после того, как неравенство концентраций понижается до величины порядка у/п. Для этого необходимо произвести лишь 47 двойных переливаний, о которых говорится в условии задачи…

Примечания:

5

'American Mathematical Monthly, 64, 1957, p. 143.

51

В одном долларе сто центов.